关于Profile 控制图的若干研究

论文总字数：37950字

摘 要

统计过程控制（SPC）是监控和诊断生产过程、产品质量的一项重要手段。在一些应用中，过程的优劣取决于因变量与一个或多个自变量之间的函数关系。profile监控就是为检查函数关系随时间变化的稳定性。本文主要介绍了参数和非参数模型下的第二阶段profile监控方法，包括线性profile、非线性profile、一般线性profile以及非参数profile等模型的过程控制问题。对于线性profile，采用EWMA控制图，克服了Shewhart图对小而持久的跳跃点预测性能不佳的缺点，该方法还可推广到多元下的一般线性profile控制图。对

于非线性profile，利用高斯牛顿迭代法构造EWMA控制图。

当自变量与因变量的关系太过复杂而无法用参数描述时，使用非参数profile的控制图十分有效。结合广义似然比检验方法构造非参数profile下的EWMA控制图。此外，对于profile内数据具有相关性时，用非参数混合效应模型描述相关下的非参数profile，将局

部线性核平滑法并入EWMA控制图中。

关键词：profile监控 统计过程控制 EWMA 非参数 第二阶段分析

Study on Profile Control Charts

Abstract

In reality, we use statistic process control to monitor and diagnose the producing process and the quality of productions, which is the most important part in manufacturing industries. In some certain applications, the pros and cons of the process depends on the functional relationship between the response variable and one or more explanatory variables. In this paper, we mainly introduce the methods of phase Ⅱ profile monitoring under parametric models and nonparametric models, including the problems of process control about linear profile, nonlinear profile, general linear profile, nonparametric profile and other models. In terms of linear model, we take use of EWMA chart. Shewhart chart is inefficient in detecting small and lasting shift points. However, EWMA performs well in this kind of problem. Also, it can also expend to multivariate general linear profile chart. For nonlinear profile, EWMA can be constructed with Gauss-Newton iteration.

If the relationship is too complicated to describe in terms of parameters, it’s more efficient to use nonparametric profile control chart. Constructing EWMA control chart of nonparametric profile with the generalized likelihood ratio test method. What’s more, when there is correlation within profiles, we use nonparametric mixed effect model to describe the data and combine local linear kernel smoothing method with EWMA control chart.

Key Words: profile monitoring SPC EWMA nonparametric phase Ⅱ analysis

目 录

摘 要 I

Abstract I

第一章 引言 1

1.1 profile监控的介绍 1

1.2 研究现状 1

1.3 各章内容简介 2

第二章 参数profile监控 3

2.1 线性profile监控 3

2.1.1 模型及估计 3

2.1.2 基于EWMA的线性profile控制图 4

2.2一般线性profile控制图 7

2.2.1一般线性profile模型及检测方案 7

2.2.2多元指数加权移动平均控制图 9

2.3 非线性profile监控 9

2.3.1 模型及估计 9

2.3.2基于EWMA的非线性profile控制图 11

第三章 非参数profile监控 13

3.1 非参数profile监控 13

3.1.1模型及假设 13

3.1.2广义似然比检验 13

3.2 非参数混合效应模型下的profile监控 15

3.2.1 NME模型的估计 15

3.2.2第二阶段非参数profile监控 17

3.2.3操作参考 21

第四章 数值模拟 23

4.1线性profile监控的数值模拟 23

4.2非线性profile监控的数值模拟 24

4.3 非参数profile监控的数值模拟 24

第五章 实际数据分析 25

第六章 结束语 26

第七章 附录 27

致谢 40

参考文献 41

2. 引言

1.1 profile监控的介绍

在许多统计过程控制(Statistical Process Control，SPC)问题中，我们所关心的产品质量已经不是简单的某个或某几个指标的均值或方差，而是要用一些自变量和响因变量之间的关系才能更好地刻画或衡量。^[1]在这样的问题中，我们得到观测值是一些回归曲线，对这样的数据监控称为profile监控。该方法是指通过观察由变量数据点构成的曲线，检查函数关系随时间变化的稳定性。^[2]在许多实际问题中有着非常重要的应用，也是当今SPC领域的热点研究问题之一。由此，选取合理的模型对于准确描述profile数据是至关重要的。

近几年，profile监控广泛应用于工业制造、金融风险等领域。它能够有效地判断过程的可控性，在异常发生前做出预警，帮助调整，恢复平稳。总体来说，profile监控的常规过程主要有以下几点：（1）选取模型；（2）确定设计点；（3）模型下参数估计与选取；（4）构造控制图；（5）监测变化。

1.2 研究现状

在已有的研究中，很多方法可以得到profile控制图，并且大多数监控图基于观测值之间相互独立的假设。然而，在现实应用中，数据通常在一定程度上具有相关性。因此，有人提出了线性与非线性的混合效应模型。需要注意的是，即使确定了该模型，仍需要靠考虑随机效应和混合效应服从的模型，另外，假设随机误差的协方差矩阵满足某种参数形式。对于研究Profile控制图的复杂性可见一斑。

幸运的是，计算机技术的高速发展对于控制图中的计算问题具有很大帮助。本课题涉及到的理论方法与相关计算切实可行。研究通常类别下的profile监控图，对于社会生产，金融体系，健康疾病及其他领域的管理与调控具有重要意义。

Profile监控在生活中实际运用非常广泛。近年来，许多学者着重于研究更一般的profile类型、更有效的监控图以及分析相应的模型假设。模型的种类千变万化，在研究中，我们通常首先选取恰当的模型：线性模型、一般线性模型、非线性模型、非参数模型、混合效应模型等等。

WILLIAM H. WOODALL在2007年的著作中系统得介绍了简单线性模型、多元和多项式模型，非线性模型。当简单的模型无法有效地描述profile的形状，文中提及可以使用含有Wavelets的模型。同时，在该文中，作者强调了在监控profile时，需要注意的4个问题：（1）仔细区分第一阶段和第二阶段应用的有效性。（2）关于包括或不包括profile内方差的这一问题的选择会产生方差。（3）注意使用能够预测profile图中跳跃低点类型的有效方法。（4）使用最简单有效的profile模型。

另外，作者也在文中提到在统计过程控制中使用到的5种方法：（1）观察维度（如“厚度”）。（2）观察“圆度”。（3）预测在关于原始样本和校正样本的QQ图中的变化。（4）p维Hotelling 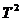方法。（5）监控“基于周期的信号”。^[3]

在已有的文献中，大多数统计过程控制是为了第二阶段的过程控制。Tsung F,Zou C, Wang Z在2007年的文章中介绍了对于第二阶段的研究，关注的对象是可以表示成多项或者多元的一般线性profile模型。并且，作者提出使用MEWMA图说作为信号图来监控一般线性模型的系数和方差。该信号图与其他文献中提出的复式图复杂程度相同，执行效果优良。^[4]另外，作者提出了3个方向完善该方法。 

随后，Tsung F等人又在2008年的文章中详细说明了在非参数回归模型下的第二阶段profile监控。文章中，LRT下的MEWMA图提供了一个有效的方法，该方法不仅解决非线性profile问题，而且对于处理模糊、失控模型引起的无法预测跳跃点类型这一问题十分有效。之后，作者介绍了诊断模型优劣的方法的三个主要方面：（1）确认变化点的位置。（2）判断方差的稳定性。（3）判断回归函数是否改变。^[5]文章最后，作者对于不同方法得到的控制图（NMEWMA,NEWMA,NM,PM）进行比较。每种类型的控制图有其自身的特点及优势，在不同模型下具有不同的表现，因而选择恰当的控制图需谨慎。

需要说明的是，本文是以在第一阶段得到较好的数据的基础上进行的分析，所以，第一阶段的分析与建模对第二阶段影响深远。

在已有的文献中，控制图大多是监控参数profile的。该类控制图假设——profile内数据相互独立，而这在实际操作中很难实现。当profile内部具有相关性，正确的模型建立和某些IC过程的参数值估计会有一定难度。忽略相关性会对监控图表的受控和失控性质带来不利影响。

Wang Z等人在2010年发表的文章中着重研究profile内数据相关下的非参数profile监控，提出了一种新的控制图——将局部线性核平滑法并入EWMA控制方式中。在这种方法下，profile内相关性可以由非参数混合效应模型描述。文中，作者使用的模型是非参数混合效应模型，该方法具有灵活的方差-协方差结构，并且适用于某些profile内相关。

1.3 各章内容简介

本文由6个部分组成。第一章主要介绍profile监控基本原理及研究现状。第2.1节重点介绍参数模型下，线性和非线性模型的设定和估计，以及推出相对应的EWMA控制图的表达式。同样的，非参数模型下，线性和非线性模型的设定和估计，以及推出相对应的EWMA控制图的表达式是第2.2节的主要内容。

非参数混合效应模型及其模型估计将在第三章中展开讨论。在第3.2.2节中，我们会提出一项新的第二阶段非参profile监控图，它融合了profile内相关及任意型设计。计算上的问题会在3.2.3中解释，而关于所提出的监控图的设计和补充方面的应用指南都在附录中有所说明。

1. 参数profile监控

2.1 线性profile监控

2.1.1 模型及估计

在许多应用中，基于科学知识及以往对于产品过程的经验的基础上，参数模型常用于刻画受控Profile的数据。由此，在这种情况下，我们通常考虑参数profile监控的相关技术。该节中，我们主要讨论线性回归模型。

在profile监控问题中，我们主要关注因变量y和自变量x之间的关系。为了监控这种关系，需要在不同时间段生产的产品中随机抽取一部分用于研究。对于第j个抽取的产品(j=1,2,....)共有n组观测值(x,y)，由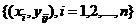表示。具体模型如下：

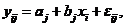i=1,2,...,n, j=1,2,... （2.1）

其中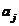，和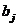分别是真实回归模型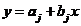的截距和斜率。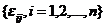独立同分布于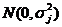。当第j个产品是受控的(IC)，假设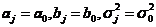。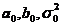分别是（2.1） 中截距、斜率和误差方差的IC值。在本节中，该模型被称为IC线性回归模型。

对于模型1，主要有一下两个假设：

剩余内容已隐藏，请支付后下载全文，论文总字数：37950字