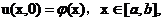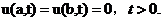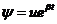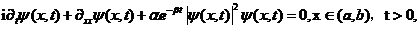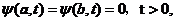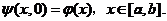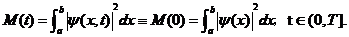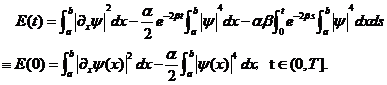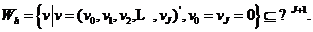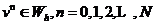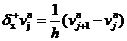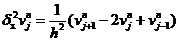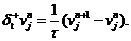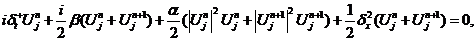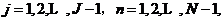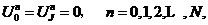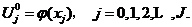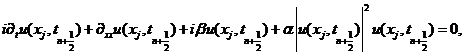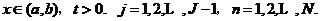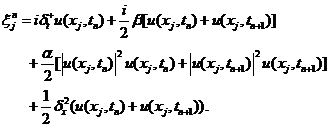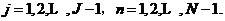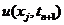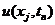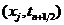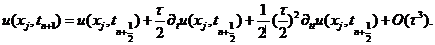论文总字数:8913字
目 录
1、引言 3
2、有限差分格式 4
3、数值分析 5
4、数值算例及其结果 8
5、总结与展望 13
参考文献 13
致谢 16
非线性耗散Schrödinger方程的一个线性化有限差分格式
何宁霞
,China
Abstract: In this paper, a type of nonlinear dissipative Schrödinger equation is numerically studied and analyzed. A linearized finite difference scheme is proposed for solving the nonlinear equation. In the practical computation, only a tridiagonal system of linear algebraic equations need be solved by using a iterative double-sweep algorithm, which means that the proposed scheme is high efficient. The local truncation error of the proposed scheme is defined and analyzed in detail by using Taylor’s expansion, it is proved to be second-order both in time and space directions. Numerical experiments show that the order of the global error is also of second order, as is consistent with the order of the local truncation error. These numerical results also show that the new scheme is stable and efficient.
Key words: Nonlinear dissipative Schrödinger equation; Linearized finite difference scheme; Taylor’s expansion; Local truncation error
1引言
非线性耗散Schrödinger(DNLS)方程
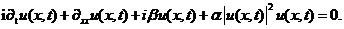 (1.1)可用来描述很多有趣的类似光脉冲在吸收型非线性光纤中的传输[1]的物理现象,其中的i为
(1.1)可用来描述很多有趣的类似光脉冲在吸收型非线性光纤中的传输[1]的物理现象,其中的i为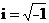 ,α与β为两个实值常数且有α,βgt;0,
,α与β为两个实值常数且有α,βgt;0,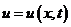 为未知复值波函数。此外在DNLS方程中,方程的第二项是色散项,方程的第三项是耗散项。标准三次非线性薛定谔(NLS)方程就是DNLS方程在βgt;0的时候得到的。
为未知复值波函数。此外在DNLS方程中,方程的第二项是色散项,方程的第三项是耗散项。标准三次非线性薛定谔(NLS)方程就是DNLS方程在βgt;0的时候得到的。
本文研究DNLS方程(1.1)的初边值问题,其初边值条件为
容易验证,在初边值问题(1.4)—(1.6)中可满足如下的两个守恒律,即总质量的守恒
和总能量的守恒
关于NLS方程的数值研究虽已有大量结果(参见[3,4,10,14,15,17]及其参考文献),而关于DNLS方程的数值研究尚不多见。文[5]中,Bao和Jaksch运用时间分裂谱方法对DNLS方程进行了数值研究,并对某些动力学行为进行了数值模拟。Delfour,Fortin与Payre[9]在文[9]中提出的有限差分格式的数值结果表明该格式在计算过程中会产生锯齿状振荡。随后,为了消除锯齿状耗散,Peranich[11]对文[9]中提出的有限差分格式进行了修改。而Dai和Nassar[7]引入一个变量代换后将DNLS方程中的耗散项消掉了。于是他们得到了一个关于新变量的无耗散的NLS方程(1.4),并在此基础上提出了一个守恒的有限差分格式。但是,文献[7,9,11]中的所有差分格式都是完全非线性隐格式。因而文献[7,9,11]中的所有差分在格式每一时间层都要求解一个非线性代数方程组,这就是说在实际的计算中大量机时要被消耗掉。Zhang,Yu和Zhao[18]为了提高计算效率,提出了一个线性化守恒差分格式。且在文[18]中,Zhang,Yu和Zhao建立了格式在L2范数下的最优误差估计,并证明了在时空两个方向上该格式为二阶精度。然而该格式是一个三层格式,不能自启动。本文对非线性项系数采用一种新的离散,构造出一类具有二阶精度的两层有限差分格式,新格式不需要自启动且具有良好的稳定性。
本文结构如下:第二部分对DNLS方程提出一个有限差分格式。第三部分运用泰勒展开对新格式的局部截断误差进行详细分析。第四部分通过数值算例测试格式的精度、稳定性和有效性。第五部分中,我们对本文的主要工作进行总结并对今后的工作进行展望。
2有限差分格式
我们取两个正整数为J与N,令τ=T/N和h=(b-a)/J分别是时空两个方向的步长,其中0lt;Tlt;Tmax,Tmax为方程解的最大存在时间。
令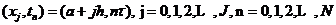 为网格点。我们令
为网格点。我们令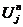 和
和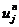 分别是
分别是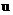 在点
在点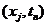 处的数值解与精确解。定义网格函数空间Wh如下
处的数值解与精确解。定义网格函数空间Wh如下
现在我们在网格结点上考虑初边值问题(1.1)-(1.3),我们给出如下有限差分格式,即
3数值分析
对初边值问题(1.1)-(1.3)在点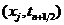 处考虑微分方程(1.1),有
处考虑微分方程(1.1),有
定义本文格式的局部截断误差为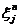 ,对本文格式用精确解代替数值解,则有
,对本文格式用精确解代替数值解,则有
剩余内容已隐藏,请支付后下载全文,论文总字数:8913字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;