论文总字数:8677字
目 录
1.引言 5
2.准备知识 7
2.1基本定义 7
2.2引理 10
3.主要结果 11
4.数值例子 16
5.总结 18
参考文献 19
致谢 21
一类广义Sylvester矩阵方程的混合条件数分析
林坤德
,China
Abstract:In this paper, we mainly study the mixed condition number analysis of a class of generalized Sylvester matrix equations. Firstly, we give the background of a class of generalized Sylvester matrix equations. Then we give the definitions and related properties of the mixed condition number. Secondly, we give the main results of this paper; i.e., the analysis of mixed condition numbers for a class of generalized Sylvester matrix equations. Finally, we give small numerical examples to prove our theoretical results.
Key words:generalized Sylvester matrix equations; Condition number analysis; Kronecker Product
1.引言
在许多领域的问题中都有涉及到广义Sylvester 矩阵方程,比如矩形域上的椭圆边值问题在离散后会出现一个Sylvester矩阵方程; 在研究常微分方程定性理论以及数值求解的隐式Runge - Kwutta方法与块方法时,也经常会遇到广义Sylvester 矩阵方程的求解问题; Sylvester矩阵方程也出现在线性统计领域中; 在控制理论及应用中也涉及到此类方程的求解,包括在极点配置、观测器以及构造Sylvester函数中。 另外,在图像恢复、模型降阶以及信号处理等领域中也会涉及到广义Sylvester矩阵方程。
广义Sylvester方程在控制理论和系统理论中有着重要的应用。 考虑下面的一般动力学线性模型
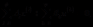 (1)
(1)
其中 以及
以及 分别表示状态向量和输入向量;
分别表示状态向量和输入向量;  以及
以及 是系统系数矩阵。 动态线性系统(1)包含如下线性系统
是系统系数矩阵。 动态线性系统(1)包含如下线性系统
 (2)
(2)
和如下二阶线性系统
 (3)
(3)
以及高阶动力学线性系统
 (4)
(4)
线性系统(2)捕捉了许多物理系统在实际中的动态行为,如参考文献[1-3]。 二阶线性系统(3)在振动和结构分析,机器人控制和航天器控制中有广泛的应用,如文献[4,6]。 线性系统(1)的极点配置和观测器设计问题也被广泛关注,如参考文献[5,6]。
本文考虑一类广义Sylvester方程:
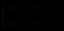 (5)
(5)
这里 且为已知矩阵,同时
且为已知矩阵,同时 是待确定矩阵,并且本文假设矩阵
是待确定矩阵,并且本文假设矩阵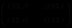 是可逆阵(
是可逆阵( 表示单位矩阵)。 显然,广义Sylvester方程(5)是有着重要应用的,如在有结构的极点配置的控制问题中有广泛应用。
表示单位矩阵)。 显然,广义Sylvester方程(5)是有着重要应用的,如在有结构的极点配置的控制问题中有广泛应用。
条件数分析对于问题本身的稳定性有着主要衡量作用。 关于混合型条件数,国内外已有很多研究成果。 比如,在文献[2]中Yiqin Lin和Yimin Wei提出了一般形式的Sylvester矩阵方程的混合型条件数; 这两位前辈也在文献[7]中对非对称Riccati方程的混合型条件数进行了研究,Landong Liu在文献[8]中也进行过类似的研究。Weiguo Wang和Nan Hao则在文献[9]中对双曲QR分解的混合型条件数进行了研究。 关于线性最小二乘问题的混合型条件数,也由Baboulin M和Dongana J在文献[6]中给出。
2.准备知识
在本文中,我们用 表示具有
表示具有 行
行 列的实数矩阵集合,用
列的实数矩阵集合,用 表示具有
表示具有 行
行 列的复数矩阵集合,用
列的复数矩阵集合,用 表示
表示 阶单位矩阵; 用
阶单位矩阵; 用 表示位于矩阵
表示位于矩阵 的第
的第 行第
行第 列的元素。
列的元素。
首先我们给出一些基本定义,如下:
2.1基本定义
定义2.1.1 广义Sylvester方程
广义Sylvester方程定义如下:
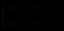
这里 且为已知矩阵,同时
且为已知矩阵,同时 是待确定矩阵。 在控制系统的很多问题中,广义Sylvester方程都与其有密切相关性,比如代数离散Ricatti方程的求解,可以通过计算矩阵束
是待确定矩阵。 在控制系统的很多问题中,广义Sylvester方程都与其有密切相关性,比如代数离散Ricatti方程的求解,可以通过计算矩阵束 的特征子空间求得,而广义Sylvester方程的解能够构成上述的特征子空间。 此外,在广义系统的模型降阶中也需要求解广义Sylvester方程。
的特征子空间求得,而广义Sylvester方程的解能够构成上述的特征子空间。 此外,在广义系统的模型降阶中也需要求解广义Sylvester方程。
定义2.1.2 条件数
条件数是指,在线性方程组 中,方程组的解
中,方程组的解 由于
由于 中产生误差而发生变化的
中产生误差而发生变化的
敏感程度。 在数学上用矩阵 的范数与
的范数与 的逆矩阵的范数的乘积表示矩阵
的逆矩阵的范数的乘积表示矩阵 的条件数,即
的条件数,即 。这里,条件数记为
。这里,条件数记为 ;
; 表示
表示 的逆矩阵。
的逆矩阵。
定义2.1.3 矩阵的转置
设矩阵 ,把矩阵
,把矩阵 的行列互换,即把元素
的行列互换,即把元素 与元素
与元素 互换位置而产生的
互换位置而产生的
新矩阵,称为矩阵 的转置矩阵,通常用
的转置矩阵,通常用 表示。
表示。
定义2.1.4 矩阵的共轭转置
剩余内容已隐藏,请支付后下载全文,论文总字数:8677字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


