论文总字数:9343字
目 录
1. 引言 3
2. 预备知识 3
3. 扩展卡尔曼滤波 4
3.1非线性泰勒展开 4
3.2扩展卡尔曼滤波的模型 5
4.扩展卡尔曼滤波仿真实验 7
5.结论 14
5.1扩展卡尔曼滤波与卡尔曼滤波的不同之处 14
5.2扩展卡尔曼滤波的优缺点 15
参考文献 15
致谢 16
扩展卡尔曼滤波及其应用
田悦
,China
Absrtact: At present, the shadow of Kalman filter is widely used in practical applications because of its powerful function, and can be used to estimate the current, past and future state of the signal by recursive method. However, Kalman filtering only provides the optimal solution for the recursive Bayesian estimation problem under normal distribution in linear systems. In real life, not all systems are linear. In this paper, extended Kalman filter is introduced, which is the most direct and natural approach to approximate optimization of nonlinear system functions. First, the normal distribution and its properties are discussed. Secondly, the nonlinear problem is transformed into an approximate linear filtering problem by linearization method, and then the Kalman filtering theory is applied to obtain the filtering algorithm for the original nonlinear filtering problem. Finally, a simulation example is given to further explain the extended Kalman filter.
Keywords: Kalman filter; Extended Kalman filter; Normal Distribution; Taylor Approximation
- 引言
卡尔曼滤波是一种线性的系统状态方程,它由系统来输入和输出数据,同时对系统的状态进行最优估计。它可以用一系列递推的数学公式来表述,提供了一种高效并且可以计算的方法来估计过程的状态,同时也可以使得估计的均方误差最小。目前已经成为了研究讨论以及仿真应用的主题。在使用卡尔曼滤波之前,我们需要了解应用它的三个前提条件。第一,应用卡尔曼滤波的系统必须是可以观测的,这样我们才可以比较观测值和估计值的偏差;第二,我们所应用的系统必须是线性系统,并且可以写出预测下一时刻状态的方程,这样才可以得出下一时刻的估计值与观测值作对比;第三,假设该系统的噪声统计特性是可以观测到的。运用卡尔曼滤波的意图就是要利用这些已知的信息来估计离散时间过程的状态变量,从而及时了解系统的运行状态以及变化。它可以有效的去除测量值中的随机误差,从而得到更加准确的实验结果,并且通过递归的算法将状态变量引入卡尔曼滤波理论中,然后按照递推公式推导即可得出新的估计值。
但是卡尔曼滤波也有一定的局限性,第一,它只可以处理线性信号过程;第二,它要求状态方程和观测方程必须都是线性系统;第三,噪声均要服从高斯分布。虽然实际生活中有许多系统都可以满足这种限制,但是在非线性系统中,系统噪声的统计特性一般都是未知的或者是实时变化的,我们只有正确的估计出系统的统计噪声,才能够进一步提升对于非线性系统数学建模和预测估计的能力,当实际系统的非线性特征偏强或者是噪声特性偏离高斯分布较大的时候,卡尔曼滤波器给出的轨迹就很难贴近于真实轨迹。为了解决上述问题,必须要建立起适用于非线性系统的滤波算法,因此便引入了扩展卡尔曼滤波。
扩展卡尔曼滤波可以更加精确的估计非线性系统的状态,从而得到较好的跟踪效果。对于这些非线性的系统,我们通常使用的处理手段是通过线性化方法将非线性模型转化成为一个近似线性的滤波模型,然后再按照卡尔曼滤波理论完成此次滤波跟踪。总体来看,扩展卡尔曼滤波的核心要素就是基于先验估计所做出的系统线性化。它的优点是可以广泛应用于非线性系统当中,并且不需要预先计算出过程噪声和观测噪声均为0时非线性方程的解。它的缺点是只可以在滤波误差以及进一步预测误差较小的时候才可以应用。目前扩展卡尔曼滤波已经被应用到各个领域,比如:目标跟踪、金融、无线通信导航、自动控制、工业等领域。
- 预备知识
正态分布是实际生活中最常见的分布之一,它是有两个参数 的连续型随机变量分布,其中
的连续型随机变量分布,其中 是均值,
是均值, 是方差,所以正态分布通常记为
是方差,所以正态分布通常记为 。 如果一个随机变量同时受到很多因素的影响,但是其中任一因素又不起到决定性作用,那么这个随机变量一定服从或者是近似服从于正态分布。
。 如果一个随机变量同时受到很多因素的影响,但是其中任一因素又不起到决定性作用,那么这个随机变量一定服从或者是近似服从于正态分布。
正态分布是通过它前二阶矩的期望和方差来确定的,假设随机变量 ,均值为
,均值为 ,方差为
,方差为 ,则随机变量的概率密度为:
,则随机变量的概率密度为:

这里|P|表示协方差矩阵P的行列式。
引理1[1] 假设随机变量 和
和 是正态分布且
是正态分布且 ,
, 则
则 ,
, 的联合分布以及y的边缘分布分别为:
的联合分布以及y的边缘分布分别为:
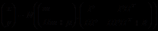

引理2[1]假设随机变量 和
和 具有联合的正态分布
具有联合的正态分布
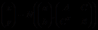
则随机变量 ,
, 的边缘分布以及条件分布分别为:
的边缘分布以及条件分布分别为:




- 扩展卡尔曼滤波
我们在讨论扩展卡尔曼滤波之前,首先要知道扩展卡尔曼滤波实质上就是线性化的卡尔曼滤波。它和线性的卡尔曼滤波在滤波器算法这个方面有着一模一样的结构,不同之处在于这二者之间的模型不尽然相同。卡尔曼滤波它的自身系统就是一个线性系统,然而扩展卡尔曼滤波它的自身系统是一个非线性系统,扩展卡尔曼滤波是将这个非线性的系统模型进行了线性化改造,这样我们才可以将卡尔曼滤波算法的理论应用在非线性系统当中。但是扩展卡尔曼滤波有一个很大的缺点就它是会发散,这是因为我们在对非线性系统进行线性化的过程中,只有被线性化的那个点附近的线性化模型和真实模型相近,离的比较远的点,它的误差就会很大,这个时候扩展卡尔曼滤波的效果就不是很好。因此线性化这个限制是我们无时无刻都要考虑的[2]。
判断扩展卡尔曼滤波器的性能是否优良需要考虑的首要因素是滤波器系统模型的线性化程度。一个越符合实际模型的线性化系统对于扩展卡尔曼滤波数据的良好输出是必不可少的。总而言之,最需要注意的一点就是线性化卡尔曼滤波器若是在无效的范围内使用,它是会发散的,一定要在有效的范围内使用,否则滤波器得到的数据将会有很大的偏差。下面我们先来介绍一下线性化非线性模型所需要用到的原理。
3.1非线性泰勒展开
假设 是正态分布的随机变量
是正态分布的随机变量 ,经过非线性变换变换为随机变量
,经过非线性变换变换为随机变量 ,假设
,假设 为正态分布的随机变量,下面考虑利用函数的泰勒展开对随机变量
为正态分布的随机变量,下面考虑利用函数的泰勒展开对随机变量 的期望和方差进行估计。设
的期望和方差进行估计。设 ,则
,则 ,
, 的泰勒展开式可以表示为:
的泰勒展开式可以表示为:
 ≈
≈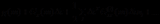
剩余内容已隐藏,请支付后下载全文,论文总字数:9343字
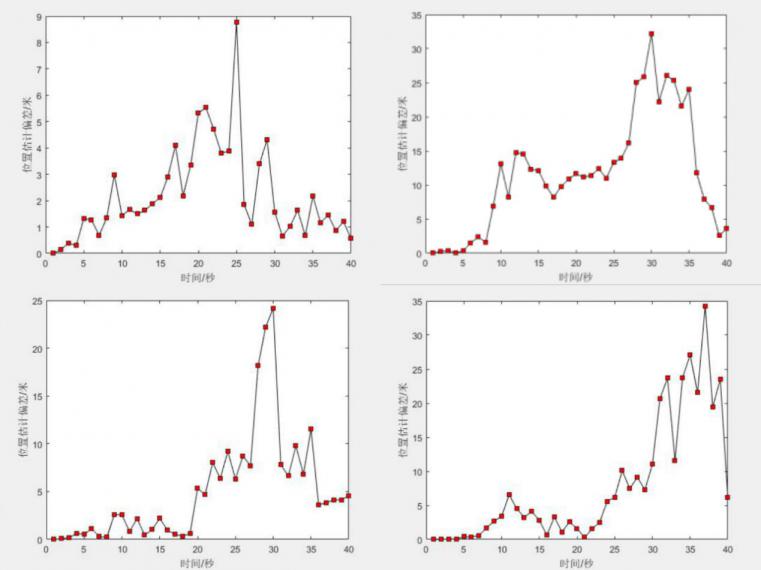
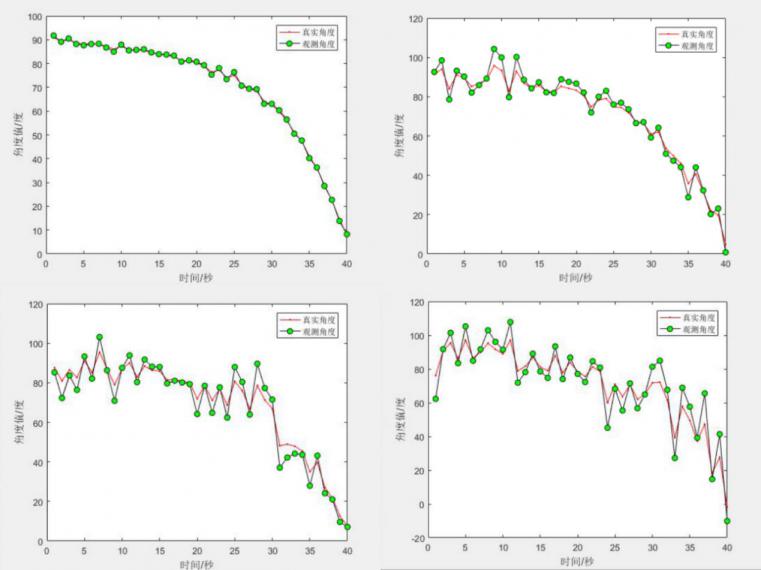
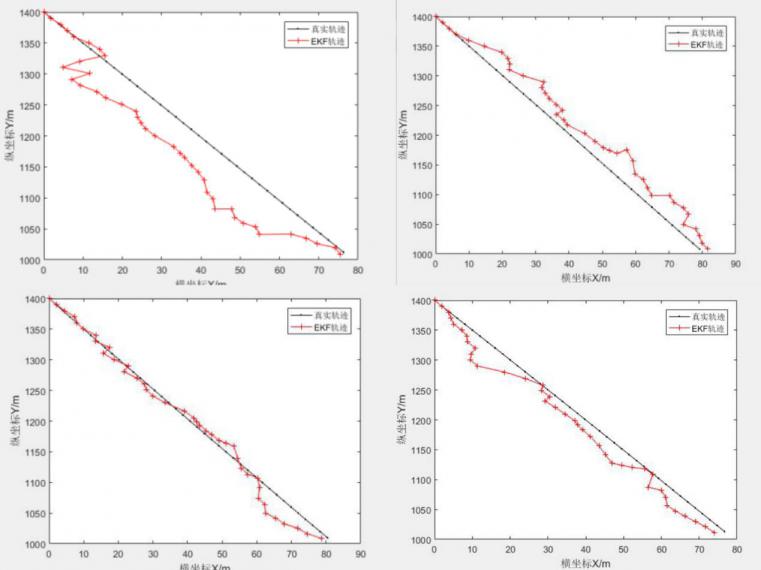
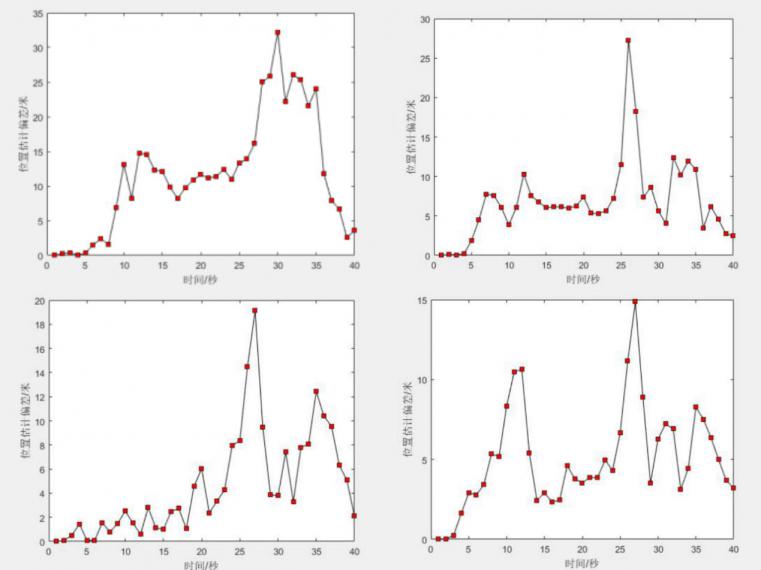
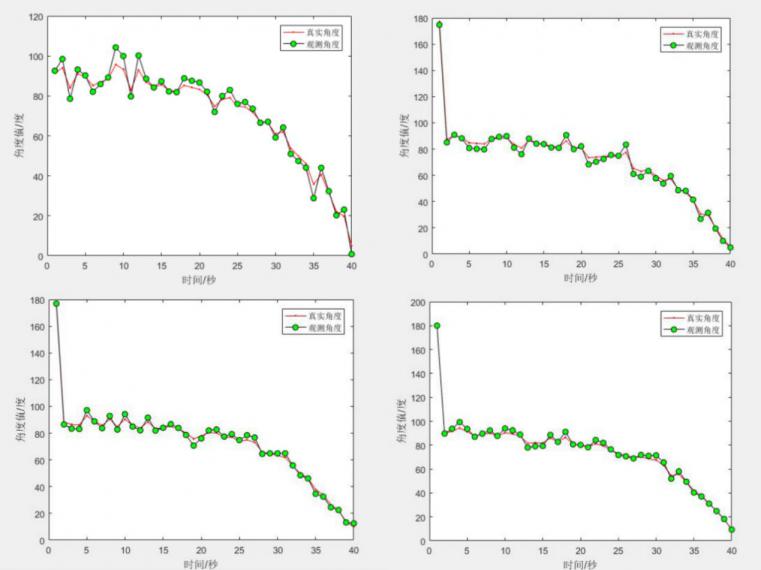
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


