论文总字数：17810字

目 录

1 引言 3

2 有限差分格式 4

3 数值分析 9

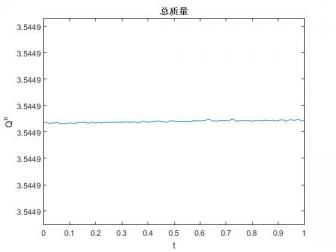
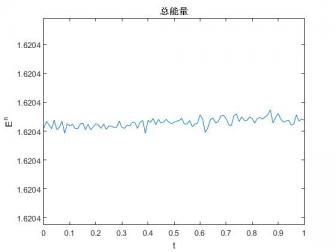
3.1 质量守恒和能量守恒 9

3.2 局部截断误差 11

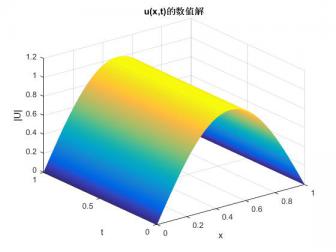
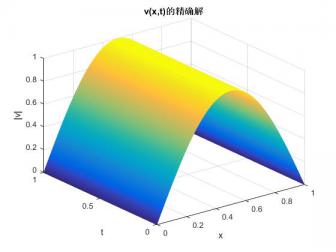
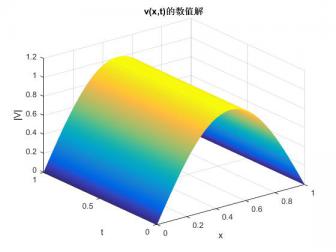
4 数值结果 15

5 总结与展望 19

参考文献 20

致谢 23

耦合非线性Schrödinger方程的紧致差分格式

成越

，China

Abstract: In this paper, we put forward a decoupled linear compact finite difference scheme for the coupled nonlinear Schrödinger equations. It is proved that, in the discrete sense, the new scheme still preserves the total mass and the total energy. We analyze in detail the local truncation error of the proposed compact scheme by making use of Taylor’s expansion, which are forth-order and second-order accuracy in spatial and temporal directions, respectively. Numerical experiments show that the convergence order of the compact scheme is second-order and fourth-order accuracy in temporal and spatial directions, respectively. In addition, the numerical results also show and verify that, in the discrete sense, the total mass and the total energy are well preserved. The collision of two solitary waves is also well simulated in the numerical experiments.

Key words: Coupled nonlinear Schrödinger equations: Linearized and decoupled scheme: Compact finite difference scheme: Mass and energy conservation

1 引言

我们知道，物理学中的许多现象，如非线性光学，量子流体学，引力，生物建模，等离子体物理等，都是用各种形式的非线性薛定谔(NLS)方程模拟的。

就非线性光学中的应用而言，NLS方程描述了单模波在纤维中的传播。根据变量的值，NLS方程允许单个和多个双曲正割解（“明孤子”），以及双曲正切解或“暗孤子”解。关于“明孤子”和“暗孤子”的数值模拟，可参考文献[1]。在许多情况下，纤维还允许多模波的传播，此时，它由耦合非线性薛定谔方程(CNLS)方程组[2,3]描述。CNLS方程组还可用来描述，非线性光学中脉冲之间的相互作用[4-6,10,37]，玻色—爱因斯坦凝聚[7-9,46]，非线性声学介质中的信号等等。

一般的CNLS方程组的表示形式如下：

(1.1)

(1.2)

其中，是两个未知的二元复值函数，线性耦合参数表示纤维的扭曲和纤维的椭圆变形所产生的影响，也被称为线性双折射[11]或相对传播常数[12]，当与具有相同符号时，和描述双折射介质中脉冲信号的自聚焦[3]，参数描述群速度色散，是交叉相位调制，参数为恒定的外部势，表示归一化双折射[13]。

本文致力于设计和分析一个具有高精度的快速有限差分格式并模拟相互作用的明孤子。该方程组满足的渐近边界条件为：

(1.3)

其初值条件为：

(1.4)

它与渐近边界条件相容。

问题(1.1)-(1.4)保持总质量和总能量守恒[48]，即

(1.5)

(1.6)

其中和分别表示的共轭和实部。

已有许多文献对CNLS方程进行了数值研究，如[4-6,14-29,38-45,47,48]。在[4]中，Sonnier和Christov提出了一个两级能量守恒但非线性的耦合有限差分格式，并模拟了CNLS方程的强耦合，并讨论了解析解和数值解。在[5，6]中，Sonnier利用[4]中给出的时空方向都是二阶精度的非线性但能量守恒的有限差分格式，研究了CNLS方程的排斥孤子碰撞动力。在[14]中，Wang等人建立了基于能量守恒的数值解的先验估计，然后建立了[4]给出的格式的最优误差估计。在[15]中，Wang，Zhang，Chen提出并分析了一个多辛有限差分格式。在[16]中，Cai提出了强耦合薛定谔系统的两个半显式多辛格式。当，时，[17]-[20]等构造了几种有限差分格式，包括Crank-Nicholson格式，线性化隐式格式，非线性隐式格式以及用于求解CNLS方程的四阶显式Runge-Kutta格式。冯诺依曼方法证明了这些有限差分格式的线性收敛性。在[21]中，Cai，Wang，Liang使用局部能量守恒和动量守恒算法来解决CNLS系统。在[22]中，Bao和Cai建立了具有内部原子约瑟夫森结的双分量玻色-爱因斯坦凝聚体基态的存在唯一性结果，为了计算这些基态，他们提出了修正过的Crank-Nicholson有限差分格式和修正过的向后Euler有限差分格式。在[23]中，用Galerkin有限元方法数值求解CNLS方程。在[24,25]中，采用时间分裂傅立叶伪谱法求解CNLS方程。在[26]中，Wang等人提出并研究了一个辛格式的差分格式，证明了在严格的网格比约束条件下范数的存在性，唯一性和二阶收敛性，并提出了求解差分格式的迭代算法。在[27]中，Sun和Zhao研究了[18]中提出的非线性有限差分格式，证明了范数的存在唯一性和二阶收敛性，并提出了另一种特别的迭代算法来求解非线性格式。在[28]中，Zhou和Chen构造了一个使用人工边界在无界区域上求解CNLS方程的数值方法。在[29]中，Wang提出了一个求解CNLS方程的非线性隐式紧致有限差分格式，证明了该方法的有效性，并建立了该格式的最优点方向误差估计。然而，[29]中提出的格式是非线性的，并且在实际计算中耦合，那么迭代是不可避免的，这意味着[29]中的非线性格式花费了CPU时间来实现。在[48]中，Wang构造了一个线性化解耦的紧致有限差分格式。受此启发，本文提出一个新的线性化解耦的紧致有限差分格式。

Fei等人在[30]中表示非守恒格式容易导致非物理的数值爆破，故对非线性薛定谔方程提出了一个新的线性化守恒差分格式，从而解决了上述问题。在[31]中，Li和Vu-Quoc也表示“...in some areas, the ability to preserve some invariant properties of the original differential equation is a criterion to judge the success of a numerical simulation.”然而，文献中的守恒差分格式几乎都是非线性的或耦合的，在实际计算中不可避免的需要迭代。因此，本文的另外一个创新点是证明新格式在离散意义下依然保持原问题的两个守恒性质，即总质量和能量守恒。本文中，关于网格函数的质量和能量泛函是用递推关系定义的。从这个角度来看，在离散意义下，已有的许多有限差分格式都可以保持原问题的总质量和能量守恒。

本文的其余部分组织如下。在第二节中，我们提出一个线性化解耦的紧致有限差分格式。在第三节中，我们证明得到，在离散意义下，新格式保持原问题的总质量和总能量守恒这两个定律。在第四节中，我们给出一些数值结果，用来验证数值解的精度和守恒律并对两个孤立波的碰撞进行数值模拟。在第五节中，我们给出一些简要的结论并对本文未解决的问题进行了展望。

2 有限差分格式

在实际计算中，选择计算域，其中和选择得足够大，以确保区间截断的影响可以忽略不计，即在这里考虑初始边界值CNLS方程的问题如下，

剩余内容已隐藏，请支付后下载全文，论文总字数：17810字

相关图片展示：