论文总字数:10320字
目 录
1引言 3
2有限差分格式及其局部截断误差 4
3离散守恒律 10
4数值实验 11
4.1数值算例1 12
4.2 数值算例2 15
4.3 数值算例3 17
5总结与展望 18
参考文献 19
致谢 20
长短波方程的两个守恒型有限差分格式
张莹
,China
Abstract: In this thesis, a numerical study of a coupled nonlinear long-wave short-wave interaction equations is carried out . By using the different discrete methods to approximate the nonlinear terms, two second-order Crank-Nicolson finite difference schemes are proposed. It is also proved that the new schemes maintain the conservation laws of the total mass and energy satisfied by the original problem in a discrete sense. Based on Taylor’s expansion, we analyze in detail the local truncation errors of the proposed schemes, which are second-order accurate in both temporal and spatial directions. Numerical experiments show that the proposed schemes have good stability and second-order convergence in both temporal and spatial directions. In addition, the numerical results also show and verify that the schemes preserve well the total mass and energy in the discrete sense.
Key words: Long-wave short-wave interaction equations; Finite difference scheme; Mass conservation; Energy conservation; Local truncation error.
1引言
长短波方程是无限维动力系统中一类影响广泛的共振模型,用于描述流体力学中的长短波相互作用,一类非线性共振波的物理现象通常也由长短波方程描述,长短波方程也被用来描述重力和毛细血管的波模型。除此之外,该方程的研究也广泛用于等离子物理学。长短波方程在描述长波和短波的共振时,短波通常用薛定谔方程描述,而长波则常用带有色散项的波方程描述,其数学形式是:
 (1.1)
(1.1)
 (1.2)
(1.2)
其中,参数 是三个正常数,短波曲线
是三个正常数,短波曲线 是未知的复值函数,长波振幅
是未知的复值函数,长波振幅 是未知的实值函数,外力项
是未知的实值函数,外力项 为已知的复值函数,外力项
为已知的复值函数,外力项 为已知的实值函数,它们在很多物理问题往往取值为零。我们考虑长短波(LS)方程的初边值问题,其初边值条件为:
为已知的实值函数,它们在很多物理问题往往取值为零。我们考虑长短波(LS)方程的初边值问题,其初边值条件为:
 (1.3)
(1.3)
 (1.4)
(1.4)
其中,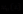 为已知的复值函数,而
为已知的复值函数,而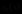 为已知的实值函数。
为已知的实值函数。
不难验证,当外力项 和
和 时,初值问题(1.1)-(1.4)满足总质量与总能量守恒律:
时,初值问题(1.1)-(1.4)满足总质量与总能量守恒律:
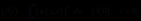 (1.5)
(1.5)
 (1.6)
(1.6)
许多文献中已给出关于长短波方程初值问题的精确解及其性质的研究,其中郭[5]讨论了关于长短波方程的全局解,Tsutsumi等[7]研究了关于长短波共振方程柯西问题的适定性。最近几年来,许多数值方法已被用于求解长短波方程。Liu和Lv[8]提出了关于长短波方程的一类拟谱方法。Chang等[9]也提出了一些数值格式,包括Crank-Nicolson隐格式(CNI), 分裂谱方法以及三层Richardson外推格式。由于高阶紧致有限差分格式通常能保持较高的精度和分辨率,经常被用来计算难以直接求解的偏微分方程(组)。王兰和段亚丽[10]首次对LS方程给出了几个高阶紧致差分格式,包括一个能量守恒格式和几个非守恒格式,这些格式对短波曲线函数的数值解在空间方向上达到了四阶收敛精度,本文在上述文献的基础上,进一步对LS方程构造出两个有限差分格式,使短波曲线函数与长波振幅函数收敛精度在时间和空间精度上均达到二阶精度,该文的结果可推广到四阶紧致差分格式,并且能在离散意义下保持原问题的两个守恒性质。
本文的其余部分安排如下:在第二部分提出了长短波(LS)方程的两种有限差分格式,并利用泰勒展开公式求证了两种格式的局部截断误差。第三部分证明了两个格式在离散意义下均保持了原问题的两个守恒性质。在第四部分中,我们进行了一些数值实验。数值实验表明:两个格式都非常好地保持了总质量和总能量守恒,而且具有较高的精度和良好的稳定性。在第五部分中,我们简要总结了本文的主要结果。
2有限差分格式及其局部截断误差
首先要网格化,取空间步长 和时间步长
和时间步长 ,其中
,其中 和
和 是两个正整数。令
是两个正整数。令 为网格点,记
为网格点,记 为
为 在点
在点 处的数值解,
处的数值解, 为
为 在点
在点 处的精确解,记
处的精确解,记 和
和 分别为在点
分别为在点 处的数值解和精确解。定义网格函数空间
处的数值解和精确解。定义网格函数空间 为:
为:

任给网格函数 ,我们引进如下记号:
,我们引进如下记号:

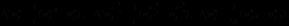
定义网格函数空间 中的离散内积和离散范数如下:
中的离散内积和离散范数如下:
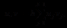

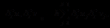 (2.1)
(2.1)
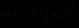

 . (2.2)
. (2.2)
剩余内容已隐藏,请支付后下载全文,论文总字数:10320字
相关图片展示:

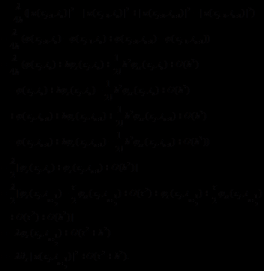
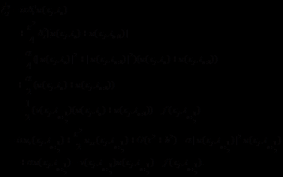
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


