论文总字数：12213字

目 录

1. 引言 3

2. 高斯过程回归 3

2.1 数据分析 3

2.2 协方差矩阵 3

2.3 核函数模型 4

2.4 超参数的确定 5

3. 数据特点 5

3.1 分散型数据 5

3.2 集中型数据 6

4. 实验结果 7

4.1 改变核函数模型 8

4.1.1 平方指数核函数 8

4.1.2 有理二次核函数 10

4.2 改变噪声系数 12

4.3 改变方差数值 14

5. 结论 17

参考文献 19

致谢 20

高斯回归过程初探

葛佩霞

，China

Abstract：Gaussian process is a set of random variables, the collection of any joint Gaussian random variables, with mean value function and covariance function determines the return process, its mean and covariance is a vector and matrix respectively, to determine the mean function and covariance function, the Gaussian process is completely sure. In this paper, the basic idea of Gaussian process regression is discussed, and the new sample points are given according to the known sample points, and the output value is predicted by Gaussian regression. Choose different kernel functions (covariance function), the change of the underlying function of the target data and data variance of noise influence factors, such as multi-angle analysis regression forecast distribution, finally sums up the law of Gaussian regression. The research shows that the selection of kernel function is very important, it characterizes the correlation of data. Among them, there are square index nuclei, rational secondary nuclei, symmetric Gaussian nuclei, linear nuclei, periodic nuclei, etc. The crucial factors are the distribution of input data, dispersion or concentration, and the correlation between predicted data and known input data.

Key words： Gaussian process; Maximum likelihood estimation; Covariation matrix, kernel function, normal distribution.

引言

数据的回归分析有很多种方法，要想实现数据的回归分析首先得清楚这类数据的大概呈态。其中高斯过程回归，主要用来回归分析一组任意有限个服从联合高斯分布的随机变量的集合。探究根据已知样本点，给予新样本点，利用高斯回归预测输出值。选择不同的核函数（协方差函数）回归分析，最终总结出高斯回归规律。高斯回归问题的数学表述为：即给定一群服从正态分布的数据，且有一定的噪声模型，因为该类数据没有具体的函数表达式,所以无法预测新数据分布。通过利用协方差矩阵来阐述数据相关性，计算求得核函数。其中核函数中参数，通过极大似然估计法确定，利用约化共轭梯度算法求最大值确定参数。最终实现回归。假设预测数据为y*，输入数据为y，下面根据高斯过程回归预测新数据的分布。

高斯过程回归

数据分析

在利用高斯过程回归时，不需要知道数据的具体表达式y，如一次的，二次的等具体形式，在高斯过程回归中，没有具体形式的表达式，已知一群高斯分布中采样出来的数据，而类似的也可以认为是从高斯过程中采样得到的一个无穷维的点。现已知观测数据与对应的函数值，对每个输入数据建模并假设服从联合正态分布

（

记为，由于观察通常是带有噪声的，为某个函数f(x)加上一个高斯噪声即

假设函数f分布为具有均值函数0和协方差函数的GP即

其性质完全由均值函数和协方差函数确定

（1）

协方差矩阵

（1）式中k(x,x’)为协方差矩阵：描述两个x相似性，若离得近则对应的k值相关性也高，即协方差矩阵是x函数，不是y函数，则协方差每个元素是两个值得一个相关度量。至此完成了基本的模型建模，而我们的任务是要对新的预测数据,求出它所对应的预测值。下面详细分析求解过程。设为训练情况的已知函数值，且设为对应于测试集输入的函数值集合，为对应于测试集输入的函数值集合。则已知数据的值y与预测值y*的联合分布为：

其中

=

=

其中，矩阵元素K（）用来度量数据之间的相关性即和之间距离的远近，K为阶对称正定的协方差矩阵；为测试点X*自身的协方差，为预测点与观测集的输入X之间的协方差矩阵；由此计算出预测值的后验分布，如下

对预测数据的估计，就用数据分布的均值函数来作为其估计值，即

=

核函数模型

高斯回归过程协方差矩阵用来刻画观测值与测试点的相关性，可以选择不同的协方差函数，但是选择正确的协方差函数很关键，应根据数据的不同分布选择不同的协方差函数。找到合适的协方差函数，计算出矩阵K,,，给定好合适的，分布就可以求出来，分布求出来，均值和方差都知道，回归问题的预测问题也就迎刃而解了。常用的高斯过程核函数如下形式

=

不同的协方差函数应用于不同的模型其中常用的协方差函数选择squared exponential(平方指数)形式即

=

根据以上可以写出加入噪声后的k(x,x’)为

=

其中l为方差尺度， 为信号方差， 参数集合即为超参数一般通过极大似然法求得。

超参数的确定

协方差函数确定了高斯过程回归，在实际中不是固定的协方差函数，而是由参数确定的一簇协方差函数，最好的拟合所给的数据并预测出新数据的前提是找到合适的协方差函数，但是协方差函数中有参数需要确定。要确定这些超参数， 采取的一般方法是极大似然估计法，即对于训练样本，根据假设

=

这里包含参数及，由此得对数似然函数

=

最大化上述对数似然函数需其梯度，梯度的计算用如下公式

=

通过求解来确定参数及。函数通过优化超参数来训练，这些超参数使用最终的预测是：约化共轭梯度算法处理无限维对象可能会很麻烦，但事实证明，我们对计算感兴趣的量只需要处理有限维对象。事实上，回答有关过程的问题可以简化为使用相关分布进行计算使用高斯过程演示简单的回归。

数据特点

对于数据的回归所选择的数据应该是有要求的。现根据数据的分散程度将目标数据的组成分为两类：一是两个分散群体数据，二是：一类集中分布的数据。分别称为分散型和集中型。当探究数据分布不同带来的影响时，我们要固定其它因素不变。在选择核函数为平方指数核函数的条件下，通过一系列实验来探究数据的不同分布所带来的影响。实验结果所得数值，采用四舍五入法并保留小数点后三位表示。

分散型数据

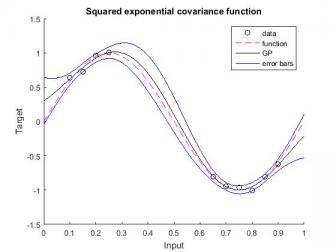
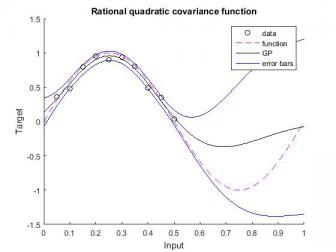
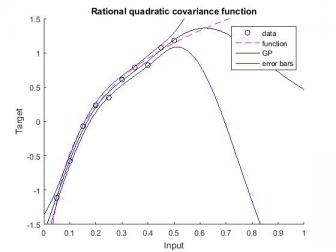
回归问题的模型：数据是由噪声产生的，GP使用平方指数协方差函数。超参数是通过对一个高斯函数进行采样来初始化的，初始化网络后使用共轭梯度的方法对其进行训练，20个周期的梯度算法。对于平方指数协方差函数，超参数是通过对一个高斯函数进行采样来初始化的,平均值为0，方差为1，超参数使用最终的预测是：约化共轭梯度算法。实验选择数据由一个输入变量X = [0.1 0.15 0.2 0.25 0.65 0.7 0.75 0.8 0.85 0.9 ]'和一个目标变量T组成。X中的值在两个分离的集群中被选择，并且目标数据是通过计算和添加高斯生成的均值为0方差为1，已知数据的个数为阶的正态分布矩阵，再乘上系数0.05的噪声所得到的。拟合情况如图1所示，红色虚线为原来底层函数图像，黑色实线为高斯回归模型输出拟合图像，蓝色实线是两个边界（图 2-16曲线含义相同）。结果偏差：0.091，噪声：0.002。

剩余内容已隐藏，请支付后下载全文，论文总字数：12213字

相关图片展示：