基于MATLAB/GUI的Wythoff游戏/博弈研究

论文总字数：20945字

目 录

1 绪论 4

1.1 课题背景及其研究意义 4

1.1.1 课题背景 4

1.1.2 研究意义 5

1.2国内外发展趋势以及研究现状 5

1.2.1国外发展趋势以及研究现状 5

1.2.2国内发展趋势以及研究现状 7

1.3本课题的主要研究内容和结论 7

2 威佐夫博弈的数学模型 8

2.1 引言 8

2.2 推导过程 9

3 MATLAB基础知识介绍 13

3.1 MATLAB的界面及功能 13

3.2 MATLAB GUI介绍 14

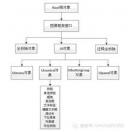
3.3 GUI层次结构 15

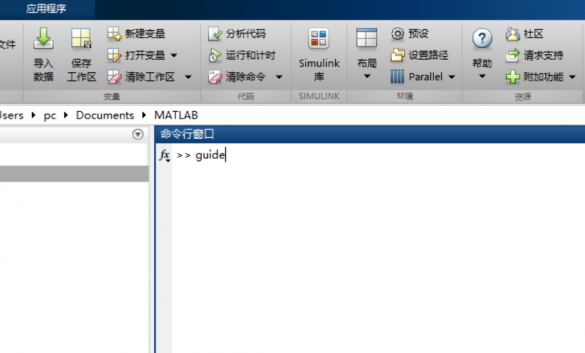
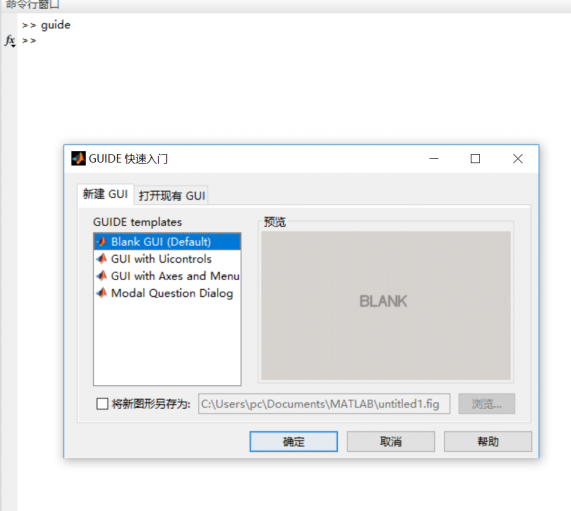
3.4 所见即所得 15

4基于MATLAB/GUI的Wythoff游戏模拟 20

4.1玩家对战模式 20

4.1.1程序设计 20

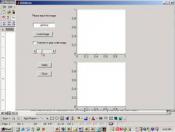
4.1.2界面展示 24

4.2人机对战模式 27

4.2.1程序设计 27

4.2.2界面展示 29

参考文献 32

致谢 34

基于MATLAB/GUI的Wythoff游戏/博弈研究

陈立

（ China）

Abstract: The Wythoff game which will be introduced in this paper is an important component and expanding part of game theory. It has a history of research and development for nearly 100 years and the related research results are mainly used in artificial intelligence and machine learning. Therefore, Wythoff game is of great significance both for the study of mathematics and for the intelligent learning of machines.

In this paper I explored the singular position of (s,t)-wythoff and then explain the design method and procedure of Matlab/gui. I focus on using Matlab/gui to simulate the Wythoff game under general rules and got two modes which are player vs player and player vs machine. Therefore, this thesis is not only the test of MATLAB software function and the realization of GUI visualization, but also the realization of Wythoff.

Key words: wythoff’s game；Impartial combinatorial game；MATLAB；GUI

1 绪论

1.1 课题背景及其研究意义

1.1.1 课题背景

首先，我们要明确该篇论文所研究的wythoff游戏实属博弈论中一种经典的博弈法，所谓博弈论就是指研讨多个个体或者集体在规定的约束条件下运用相关方面的策略方法，在对局中施行计谋以达到最佳的行动效果的学科^[1]。

其实，略经研究就会发现我国古代早就产生博弈论的发展萌芽，首先比较著名的一部历史著作就是人尽皆知的《孙子兵法》，可以说，《孙子兵法》就是一部具有重要意义的博弈论文献。而且，不光是孙武，在中国历史上的博弈高手还有许多许多：如十六国时期的著名政治家王猛，以及之后的岳飞，成吉思汗等人^[2]。之所以列举这些可称之为“博弈家”的伟大人物，就是想说明：历史滚滚向前，无数仁人志士，英雄豪杰早就告诉我们，世间万物的一切都处在博弈当中。各种文化相互碰撞，竞争发展，到最后无论是本土文化还是移民文化亦或是少数民族文化总是强势者胜。

在西方国家，博弈论同样有着蓬勃的发展，18世纪初就已经开始出现研究博弈论的相关文章，然而可惜的是，博弈论始终没有形成完整的思想和方法论体系，学者对博弈论的研究仅仅停留在研究象棋，桥牌，赌博中的胜负问题，直到20世纪初博弈论才正式发展成一门学科。

1940年到1950年间，博弈论的研究逐渐开始热门，博弈论得到了充足的发展，著名数学家纳什第一次对博弈类问题进行深入研究，在某些方面如非零角度有了长足的研究成果^[3]，现在看来其关于博弈论的研究论文《非合作博弈》萌发了非合作博弈理论的最初思想。

1950年至1980年间，博弈理论在各个方面的应用呈现百花齐放的态势。尤其需要提及的是海萨尼关于不完全信息博弈理论^[4]，这被认作是一个里程碑式的成果。关于进化博弈论的“进化稳定策略”^[5]等概念的提出表明了进化博弈论开始进入新的研究阶段，同时博弈理论在经济方面的应用和经济学理论的博弈论革命中起了不可忽略的作用。

1980年至今，博弈论的发展逐步趋向完备，一些比较著名的博弈理论如“拍卖理论”、“经济理论”等开始被引入经济、化学、生物、数学、社会学等多门学科的学术研究中^[6]。

1.1.2 研究意义

其实，学习和研究博弈论是我们探究一种理解并思考世界的重要步骤。应当认为，博弈论对研究者个人思维发展和生活指导十分局限，毕竟一个人并不能在生活的方方面面，在与人交往的时时刻刻保持以一种博弈的思辨的思维看待周遭事物发展。

然而，对于一些社会性、国家性团体而言，博弈论则极为有效地提示了一种思考维度或者称思考方式，成为人们手中分析现实问题并提炼出一般模型的重要工具^[7]，无论是FCC(美国联邦通讯委员会)拍卖案例^[8]还是英国电力公司反垄断案例^[9]都深刻的说明了博弈论的精深以及巧妙运用博弈论所能带来的巨大利益和高值回报。而本篇论文所要研究的wythoff博弈在博弈论中又是非常重要的组成部分，其意义也就不言而喻了。关于wythoff博弈的研究还有一个小小的彩蛋，就是在研究奇异局势的一般性过程中，竟然神奇的出现了1.618，如你所知，黄金分割率的数值0.618，不知这是不是也是一个“奇异”的巧合^[10]。

1.2国内外发展趋势以及研究现状

1.2.1国外发展趋势以及研究现状

Wythoff游戏起源于尼姆游戏^[11]，简单的尼姆游戏规则可以这样进行表述：假设有两名玩家进行游戏，一共有n堆石子，并设定它的编号依次为1到n,每一堆石子堆都有若干个石子。当两名玩家进行游戏时，允许抉择任意一堆石子，从中拿取石子，但是其个数也有一定要求，首先不能为0，即这名玩家不可以不选择，并且至多拿取该堆石子所有石子，两名玩家轮流拿取，判负的规则为：当玩家无石子可取时判负。W.A.wythoff对尼姆游戏的规则进行修改进而得到了Wythoff游戏^[12]，其规则可描述如下：限制石子堆数为两堆，玩家每次可以取其中一堆或者两堆，从两堆中取石子数必须一样，先取完的玩家获胜(此条规则是最先的也是最常用的游戏规则，因此称为Normal规则，后来又有学者在Normal规则下相关研究已经较为透彻的基础上反向思维，将胜利的规则变为先取完的玩家判输，并称之为规则^[13]，本文不着重探究Wythoff游戏的数学背景，故而只模拟Wythoff博弈的普通游戏模式，倘若读者有兴趣可借阅本文附录中的参考论文)。可见，这种情况下Wythoff游戏是较为复杂的。

学者Connell于1959年在他的论文中第一次对Wythoff游戏关于石子的移动方法进行限制^[14]，由此得到新的威佐夫模型并称之为K·Wythoff游戏：（1）玩家可以选择其中一堆石子，从中拿取k的整数倍个石子。（2） 玩家可以从两堆石头中同时移走同样多的石头（其中k为某个提前规定的正整数）。我们可以看出当k=1时，k·Wythoff游戏也就变成了Wythoff游戏，对此规则下的游戏Connell给出了比较完备的结论，他得到了所有的奇异位置（注：奇异位置可以理解为当出现该局势时，只要某一玩家按照合理规划的方法进行博弈就可以确保胜利，因此对于威佐夫博弈来说，得到相应规则下的奇异位置就等价于解决了相应的威佐夫博弈）。

1998年，学者A.S.Fraenkel在Connell的研究基础上对K·Wythoff进行了进一步拓展，他开拓性的创造了（s,t）-Wythoff游戏，其规则作如下简述：在游戏开始前先规定两个正整数，分别记为S和T(S≥1，T≥1)。规定玩家的移动方式有两种：（1）可以选择任意一堆石子堆，和其他游戏一样，玩家从中抓取不为0个石子。（2）从两堆石子中抓取不一样的数目个石子，倘若抓取的石子个数分别为m和n,则m和n满足0lt;mlt;n≤ms t,可见它打破了从两堆石子拿取石子时必须相同的规则。作者在论文中不仅详细论述了（s,t）-Wythoff游戏的奇异位置而且还通过多项式计算出了相关的精确度。

2004年A.S.Fraenkel又一步拓展了wythoff游戏——Function-Wythoff’s游戏，其规则可定义如下：（1）从两堆石子中选定一堆石子，从中拿取任意数目的石子。（2）同时从两堆中抓取石子，其中一堆抓取kgt;0个石子，另一堆抓取lgt;0个石子，并约定|k-l|=|(x₀-x₁)-(y₀-y₁)|lt;f(x₁,y₁,x₀)(函数f是依赖于x₁,y₁,x₀的一个实值约束函数)。可以看出，作者主要将|k-l|进行约束，让其强调了两个位置：分别为先前位置（x0,y0）和目标位置（x1,y1）。

2009年E·Duchene和A.S.Fraenkel两位学者利用集合的形式限制了Wythoff游戏并定义为Wyt_k游戏^[15]，即规则变为了：（1）玩家可以从两堆石子中任选一堆，从中拿取任意数目个石头。（2）玩家从两堆石子中取走同样多的石子，但是其数目受到规定的集合限制。可以看出该规则进一步限制了Wythoff游戏的拿取规则，在论文中两名学者借助特定的函数进行计算分析，同样得到了Wy游戏的所有奇异位置，顺利完成了对该游戏的研究。

剩余内容已隐藏，请支付后下载全文，论文总字数：20945字

相关图片展示：