论文总字数：17499字

摘 要

本文是对货运航线分包这一实际问题的建模与算法研究。研究问题是，货运航线的招投标中设有n条航线，m家公司根据自身情况对若干条航线进行投标；因航线数量大，需根据投标情况，将货运航线分成一些航线包，每个航线包都含有若干条货运航线，且至少有3家公司参与投标。目标是根据公司投标航线的情况将航线合理分包，包数尽量少且每个包内包含的航线数尽量平均。对于该问题，目前已有的优化算法，例如分枝定界法和Gomory割平面法，并不能很好地解决这个问题。本文在讨论这个问题时，从两个角度分别给出了建模的思路。第一种是利用二部图完全子图点覆盖的思路进行建模，并提出相应的启发式算法，给出了计算结果和分析。发现本算法在分包数上做到了分包数尽量少，但是每个包内的航线数非常不均匀。第二个思路是基于整数规划的建模，并在此基础上提出的启发式算法，给出了相应的计算结果和分析。这个算法的计算结果相对完善的同时满足了分包数尽量少和包内航线数尽量平均的要求。

关键词：

航线分包；整数规划；二部图覆盖；启发式算法

Research on the algorithm of freight transportation routes subcontracting problem

Candidate: Lun Dai Supervisor: Xiang Yin

Abstract：

This paper is a research on the modeling and algorithm of the actual problem of the freight transportation route subcontracting. Research question is that according to their own situation to several routes bidding, cargo airlines bidding with n routes and m companies. The freight routes into some routes packets according to the bidding because of the large number of routes. Each route packets contains several freight routes and at least three companies will participate in the bidding. The target is the number of packages as far as possible and each packet contains the route number of the average, according to the company bid route situation routing reasonable subcontract. For this problem, the existing optimization algorithms, such as the branch bound method and the Gomory cut plane method, are not well solved. In this paper, two modeling ideas are given to discuss this problem. The first one is to model the idea that the full sub graph of the two map is covered, and the corresponding heuristic algorithm is presented, and the results are given. It is found that the number of the algorithm can be as few as possible, but the route number in each package is very uneven. The second idea is based on the integer programming, and the heuristic algorithm is presented, and the corresponding results are given. The results of the algorithm are relatively perfect, while the number of the sub packets as well as the average number of routes within the package are met.

Key words：

Route planning; Integer programming; Graph covering; Heuristic algorithm

目录

第一章 绪论 5

第二章 图论及整数规划基础理论 7

2.1 二部图覆盖模型 7

2.1.1二部图的基本概念概述 7

2.1.2航线分包问题图覆盖模型建立 7

2.1.3二部图完全子图点覆盖问题常用算法及困难 8

2.2整数规划模型 9

2.2.1整数规划问题研究现状 9

2.2.2航线分包问题整数规划模型建立 10

2.2.3整数规划常用算法及困难 10

2.3启发式算法概述 13

第三章 航线分包问题的启发式算法设计 14

3.2整数规划模型启发式算法思路与描述 14

3.3算法实现与分析 15

3.3.1模拟数据 15

3.3.2算法实现及分析 16

总结与展望 22

致谢 23

参考文献 24

附录A航线分包问题图覆盖模型matlab程序

附录B航线分包问题整数规划模型matlab程序

附录C航线分包问题数据模拟随机矩阵matlab程序

第一章 绪论

随着社会经济的发展以及科学技术的进步，越来越多的各行各业决策者开始认识到，科学的决策对于企业成功的重要性。继而，人们开始研究和使用一种行之有效的计量分析工具来进行复杂的决策，运筹学。运筹学^[1][1]是现代管理学中的重要分支，兴起于20世纪30年代初，主要目的是为管理人员提供决策时的科学依据。该学科融合了实分析、矩阵论、随机过程、离散数学、算法基础、统计、数学建模等数学知识，从实际问题中抽象出具体的模型，并寻找最佳或近似最佳的解答。

运筹学的具体内容包括：规划论、图论、决策论、对策论、排队论、可靠性理论等。例如，工程中怎样设计参数，使得设计方案既满足要求又能降低成本；资源分配问题中，怎样合理分配有限资源，使得分配方案既能满足预算要求，又能获得好的经济效益；生产计划安排中，选择怎样的计划方案才能提高产值和利润。这样的问题在日常生活中非常常见，而实际应用推进着运筹学的不断进步与发展。

运筹学研究的基本特点是：定量化，模型化，最优化。^[2][2]定量化是指对所研究的问题进行分析，找出问题中影响因素之间的定量关系。模型化是指，根据实际问题的性质与类型，建立合适的准确的模型来描述。最优化是指，在模型的基础上，应用各类数学知识，运算找出最优解或者最优方案。本文中，研究的内容，就是以运筹学为背景的具体问题的建模以及算法求解。

商品快速流通的社会中，人们对运输速度以及运输安全程度的要求不断提高，航空运输在运输系统中的重要性也就不断提高。因此，与航空运输相关的数学问题也就得到更多人的重视。这里将要讨论的问题是航空运输整个阶段中的一个重要部分，并将优化的思想应用其中的货运航线招投标问题。具体而言，可将所有项目集中打包，比如500条航线，中标者得到所有的业务，但这样做会迫使服务提供商对于价格对其没有吸引力的业务进行投标。他们可能只分包500条航线中的50条。招投标优化技术使供应商可以选择能优化其成本结构的业务，从而让供应商提供给最低的价格。由此可以看出解决好航线分包问题，无论对于国家发展或投标公司竞标都有非常重要的意义。

在这个研究过程中，我们暂时不考虑市场以及其他因素，仅根据公司的投标情况进行合理分包，目的是使得分得的包数尽可能少，且每个包中的航线数尽可能平均。货运航线的招投标过程中，设有n条航线，m家公司根据自身情况对若干条航线进行投标；因航线数量大，需根据投标情况，将货运航线分成一些航线包；每个航线包都含有若干条货运航线，且至少有3家公司参与投标。建立适当的模型，规划出合理的分包模式，使得对n条航线的分包得到的包数最少。并根据建立的模型设计合理的启发式算法。

航线分包问题可以看作是一个组合优化的问题，目前在处理大型数据的组合优化问题时通常采用分枝定界法或割平面法^[3][3]，但是通过后文的分析可以看出，这个实际问题给出的数据量过大，这两种方法都不能很好的解决这个组合优化的问题。

本文从两个角度分别建立了相应的模型，并设计出相对于两种模型的启发式算法。第一种是基于二部图点覆盖的算法，将全部航线划分为若干个航线包，且每个航线包一定要至少有三家公司投标这个问题，转化为，求解这个公司航线投标二部图的最大完全二部子图，这个最大完全二部子图就是所求的一个航线包。第二种基于整数规划模型的启发式算法，我们考虑从航线的角度出发，从全部的航线中抽取一部分航线，作为一个航线包，使得每个航线包都至少有三家公司投标。抽取的过程是从投标数最多的航线开始与后面的航线进行合并，直到得到的航线包只有两家公司投标了之后，输出合并前的航线包，这样就得到了一个分包。

在本文中，第二章主要讨论两种思路的已有算法分析以及航线分包问题的新的算法的建立过程。第三章主要讨论基于两种模型的启发式算法设计以及Matlab实现。并且给出了关于两种算法的计算结果分析以及算法改进思路与方向。

第二章 图论及整数规划基础理论

• 1. 二部图覆盖模型

2.1.1二部图的基本概念概述

图论^[4][4]是以图为研究对象的数学学科。其中用点表示研究对象，两点之间的连线表示对象之间的特定关系。图论的历史发展基本分为三个阶段：

第一阶段是从1736年到19世纪中叶。其中，最具代表性的成果是数学家欧拉于1736年解决的哥尼斯堡七桥问题。

第二阶段是从19世纪中叶到1936年，此时图论主要研究一些实际的游戏问题，例如四色问题，博弈问题、Hamilton环游世界问题等。同时出现了以图为工具跨领域解决一些实际问题的成果。1847年，德国物理学家，基尔霍夫，将图论中树的理论应用于电网络方程组研究。1936年匈牙利数学家哥尼格出版了《有限图与无限图的理论》，这是第一部专门讨论图论的著作，同时也标志着图论成为一门独立的数学学科。

第三阶段是1936年之后，随着经济发展，电子计算机的应用，生产管理、交通运输、军事、计算机和通讯网络等方面大量问题的出现并且大规模问题的计算机求解，极大地促进了图论发展。目前，图论在物理、化学、计算机科学、运筹学、电子学、信息论、网络理论、社会科学及经济管理等很多学科领域中，都有广泛的应用。另外，关于图论理论证明的方面，在二十世纪以后也有了很大发展。这个方向的主要分支有随机图论、超图理论、极值图论、算法图论和网络图论等。

以下是本文将要用到的图论中的相关概念：

定义2.1 （二部图）：设和是的定点子集，使，且的每一条边的一个端点在中，另一个端点在中，则称为二部图，记作。

定义2.2（完全二部图）：如果中的每一个顶点都与邻接，则称为完全二部图。又有，，其中表示集合中元素的个数，则完全二部图用表示。

定义2.3（子图）是图的子图，如果有,，且中的边的重数不能超过中对应的边的重数。

定义2.4（覆盖与最小覆盖）：设K是的一个子集，如果图的每条边至少都有一个端点在K中，则称K是的一个覆盖。如果中没有合适的覆盖，则称K是的最小覆盖。

2.1.2航线分包问题图覆盖模型建立

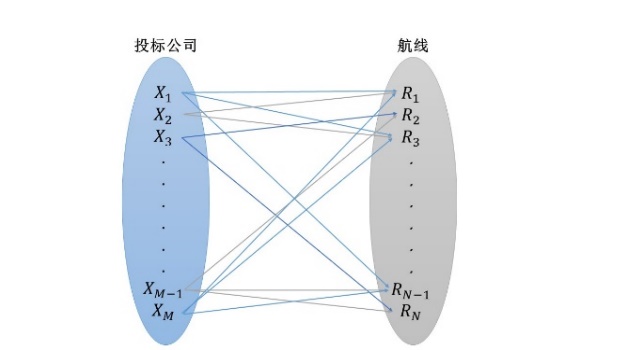
建立一个二部图，其中顶点集X中，每一个顶点表示n家公司中的一家，顶点集Y中，每一个顶点表示m条航线中的一条。则，如果第i家公司投标了第j条航线表示为，则公司对应顶点与航线对应顶点相连，即将X中的第i个顶点与Y中第j个顶点相连，边的集合为E，即。这样，根据所给数据的公司与航线投标情况，就可以得到一个表示公司投标航线情况的二部图。具体的表示如下图所示：

剩余内容已隐藏，请支付后下载全文，论文总字数：17499字