论文总字数:8567字
目 录
1 绪论 3
1.1本文基本概念和所研究的问题 3
2 循环矩阵的性质 4
2.1 引言 4
2.2 循环矩阵的性质 4
2.3 循环分块矩阵的性质 6
2.4 分块循环矩阵的性质 8
3 循环矩阵的计算 12
3.1 引言 12
3.2 循环矩阵的行列式的计算 12
3.3 循环阵的特征值和特征向量的算法 13
3.4 循环矩阵的逆的计算 14
总结与讨论 18
参考文献 19
循环矩阵及广义循环矩阵性质
孙思明
,China
Abstract:Circulant matrix is a special class of matrix,it is applied in modern science and engineering.In this paper, the circulant matrix is introduced and some of its basic properties are analyzed. The concept and properties of generalized circular matrix are obtained according to its structural characteristics.In the end,the computing method of the determinant, characteristic value, characteristic vector and its inverse of the circular matrix are simplified by the property of the circulant matrix.
There are three main parts in this paper:
Firstly, we briefly introduce the background knowledge of the circulant matrix, including its development history and some achievements.
Secondly, we obtain the circular block matrix and the block circular matrix by extending the properties of the circulant matrix, and some good results are obtained.
Finally, we give the necessary and sufficient conditions for the existence of the inverse matrix of the circular matrix and two classical inverse algorithm based on the algorithm of the circulant matrix.
Keywords:circulant matrix;the property of the circulant matrix;generalized circulant matrix
1 绪论
1.1本文基本概念和所研究的问题
矩阵是现代数学中的一个不可或缺的基础概念,它在分析数学、代数学、计算数学以及经济学中都扮演着一个不可或缺的重要角色.矩阵最初是从实际生活问题中抽象概括得出的一个理论概念,在矩阵形成之初,它仅仅是充当了一种计算工具.但随着数学研究的深入,数学理论体系的不断扩充和发散,矩阵已然成为了一门独立而又重要的数学分支,那就是我们常说的矩阵论.为一个独立的数学概念,文章lt;lt;矩阵论的研究报告gt;gt;,首次地提出了要将矩阵发展为一个独立的数学概念,在这片文章中,矩阵被总结阐述为了一个理论系统,体系中定义了矩阵的相等、矩阵间的运算法则、矩阵的转置以及逆矩阵等概念.矩阵理论在概率统计、数值分析、控制理论、信息科学与技术、与工程等 中常常有着矩阵理论的实际应用.
中常常有着矩阵理论的实际应用.
在本文中所讨论的循环阵是矩阵家族中非常特殊的一类,它有着一系列良好的性质,同时它在现代科技工程中也有着广泛的应用,如物理学、电磁学、编码理论、结构计算 、自回归滤波器设计、计算机工程等领域.
、自回归滤波器设计、计算机工程等领域.
循环阵的概念从上世纪五十年代便被提出,自此之后,广大的数学工作者对它的性质结构进行了大量的研究探讨,并得到了有关循环阵行列式的算法、循环阵的性质、循环阵的逆的算法等众多优秀的结论 .然而,虽然关于循环阵已有很多研究成果,但关于循环分块阵和分块循环阵的研究却非常少见.同时,在处理实际问题时又常会遇到此类矩阵的问题,比如电磁波散射
.然而,虽然关于循环阵已有很多研究成果,但关于循环分块阵和分块循环阵的研究却非常少见.同时,在处理实际问题时又常会遇到此类矩阵的问题,比如电磁波散射 中的分块循环阵计算问题.循环分块阵与分块循环阵既有分块阵的良好的性质,同时又有着循环阵的特殊结构,这两种特殊矩阵的性质值得我们做出深入的研究.
中的分块循环阵计算问题.循环分块阵与分块循环阵既有分块阵的良好的性质,同时又有着循环阵的特殊结构,这两种特殊矩阵的性质值得我们做出深入的研究.
1.2 本文的研究工作与内容安排
本文通过分析研究国内外相关资料,在归纳总结循环阵的定义、性质的同时,推广并证明了循环分块阵与分块循环阵的性质,并且根据推广证明得出的性质简化了已有的一些与循环矩阵相关的计算方法.
在文章编写之初,本人搜集了大量的有关于循环矩阵、循环分块矩阵和分块循环矩阵的研究资料.并从大量的中外文献的学习中,相对充分地了解了有关于循环矩阵的研究历史和国内外研究现状,同时对循环矩阵理论体系有了一定的印象.之后又对所搜集整理而得的各种资料进行梳理归纳,在总结前人的研究成果的过程中,系统地学习了循环矩阵的理论知识.最终对循环矩阵的性质进行归纳和合理的推广延伸,分析研究出了循环分块阵与分块循环阵的性质.
本文结构如下:
第二章:从循环矩阵的性质出发,将其性质推广到循环分块阵和分块循环阵;
第三章:梳理总结了一些与循环阵有关的算法,并给出了两种较为简便的求循环阵逆的算法.
2 循环矩阵的性质
2.1 引言
循环矩阵是一种带有特殊的结构特征的矩阵,它有着很多有趣的性质.众多国内外数学爱好者、数学学者在对其探讨研究的过程中,发现了很多优秀的结果,而这些研究成果使我们在计算与循环矩阵有关问题时变得更加简洁快速.
循环阵和基础循环阵的定义分别在文献 和文献
和文献 中被给出.同时文献
中被给出.同时文献 又对循环阵的性质做了系统性的分析总结,并给出了循环阵关于矩阵的加、减、乘、以及转置和当矩阵的逆存在时的求逆运算封闭的结论.在本章节中,我们通过分析循环阵自身结构特征,得出了两个循环阵的判定定理,同时也利用了这两个定理对循环阵的性质进行了较为详尽的证明.
又对循环阵的性质做了系统性的分析总结,并给出了循环阵关于矩阵的加、减、乘、以及转置和当矩阵的逆存在时的求逆运算封闭的结论.在本章节中,我们通过分析循环阵自身结构特征,得出了两个循环阵的判定定理,同时也利用了这两个定理对循环阵的性质进行了较为详尽的证明.
文献 和文献
和文献 分别提出了循环分块阵和分块循环阵的概念,我们将这两种相类似的特殊矩阵阵统称为广义循环阵.在本章中,我们分析研究了广义循环阵,并以此为出发点,推广了循环阵的性质.最终得出了广义循环阵对于矩阵的加、减、乘法、转置以及当矩阵的逆存在时的求逆运算封闭的结论.
分别提出了循环分块阵和分块循环阵的概念,我们将这两种相类似的特殊矩阵阵统称为广义循环阵.在本章中,我们分析研究了广义循环阵,并以此为出发点,推广了循环阵的性质.最终得出了广义循环阵对于矩阵的加、减、乘法、转置以及当矩阵的逆存在时的求逆运算封闭的结论.
2.2 循环矩阵的性质
定义2.2.1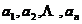 设
设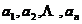 为数域
为数域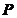 上
上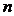 个数,则
个数,则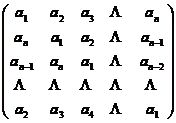 矩阵
矩阵
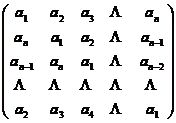
称为数域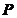 上的循环矩阵.简记为
上的循环矩阵.简记为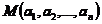 .
.
定义2.2.2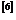 称矩阵
称矩阵 为一个基础的循环阵,
为一个基础的循环阵,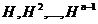 为循环阵的一个基本序列.
为循环阵的一个基本序列.
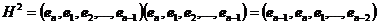
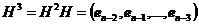
... ...
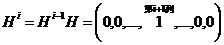 .
.
其中,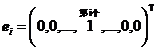 .
.
引理2.2.3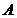
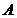 为循环阵的充要条件为
为循环阵的充要条件为 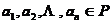
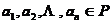 ,使得
,使得
剩余内容已隐藏,请支付后下载全文,论文总字数:8567字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


