行列式在解析几何中的应用

论文总字数：10318字

目 录

0、引言.....................................................................3

1、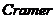法则.............................................................3

1.1定义...................................................................3

1.2应用...................................................................3

2、齐次线性方程组的几何运用...........................................7

2.1齐次线性方程组有非零解的几何运用.......................................7

2.2齐次线性方程组在空间几何中的运用.......................................9

3、行列式的几何意义...................................................11

3.1一般行列式的几何意义..................................................11

3.2特殊行列式的几何意义..................................................12

3.3特殊行列式的几何意义的运用............................................13

3.4行列式与几何方法的优劣性..............................................14

4、用行列式证明向量运算的一些性质.................................15

4.1向量积的反交换律......................................................15

4.2向量积的结合律........................................................15

4.3向量积的分配率........................................................16

5、结论....................................................................16

参考文献................................................................. 16

致谢...................................................................... 18

行列式在解析几何中的应用

徐秋阳

，China

Abstract：In this paper,we mainly talk about the application of determinant in analytic geometry.That is to say,we analyze the problem from three aspects that named non homogeneous linear equations,homogeneous linear equations and determinant.The conclusion that we can draw from this point is that determinant plays an important role in solving problems of spatial geometry.The analytic geometry is mainly used to study the space geometry and three-order determinants are often needed.The determinant can also make the problem in analytic geometry substantial.In a word,we discuss the application of determinant in analytic geometry and the geometric meaning of determinant from the Cramer rule,linear equations and determinant itself.

Key words：Analytical Geometry；Cramer rule；Linear Equations；Determinant.

1. 引言

在学习解析几何的过程中，往往有许多我们难以描绘的空间模型，这是抽象的，不便于描述的，这就对我们的解答产生了困扰，如果可以将复杂的图像转化为简单的公式运算，那将为解析几何的发展提供许多帮助，而行列式及其相关运用就可以做到这一点.而且，行列式可以将原本抽象的解析几何问题转化为可以写在纸上的公式，并且通过行列式自身的定义以及定理来解决解析几何问题，同时，行列式也不限于三阶，这就可以看作是空间几何的延伸，让只局限于三维空间的空间几何问题拓宽到多维，运用好其中的一些定理，可以更加方便地解决解析几何问题中不能解决或者难以解决的多阶问题.总结地说，行列式简化了解析几何中的部分问题，是将抽象的图形实体化的一种表现方式.本文主要研究可以通过行列式以及线性方程组这两方面的的定理来解决的解析几何问题.

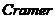1、法则^[1]

根据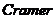法则讨论共线，共面问题

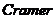法则研究了方程组的系数与该方程组的解是否存在之间的关系，如果存在，也能判断解是否唯一.即利用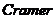法则判断一个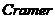阶的线性方程组是否存在解以及存在解时解的个数，可以通过将线性方程组的系数转化为行列式来进行验证.总体来说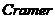，法则沟通了线性方程组与行列式之间的联系，可以将线性方程组顺利地转化为行列式进行运算.下面，笔者将从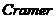法则的定义以及定义的延伸来探讨其在解析几何中的意义以及一些实例.这里主要先讨论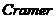法则在非齐次线性方程组中的应用.

1.1 定义

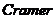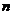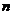定理 1.1 (法则)^[2] 如果含有个方程，个未知数的非齐次线性方程组的

系数行列式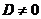，那么，方程组的解为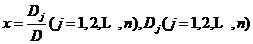，其中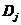，是指把行列式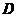中的第列元素替换成常数项，而且其余各列元素保持不变的情况，所得到的新的行列式.

这个定理毫无疑问是最基础的，应用面也是最广的，下面，就让笔者来说说它最基本的一些实例应用.

1.2 应用^[3]

线性方程组与行列式在几何中最直观的表现就是两点共线，三点共面的问题，这也是几何中最基础的问题，下面，笔者将通过法则在线性方程组与行列式中的定理，来证明下列几何问题.

1.2.1 2点确定的直线的方程

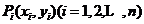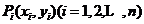定理1.2.1 平面上通过横坐标且互不相同的个点的曲线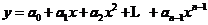有且仅有1条.

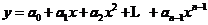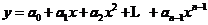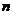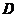证明 把个点的坐标分别代入曲线方程中，得到含个方程，个未知数的非齐次线性方程组以及其系数行列式:

， .

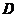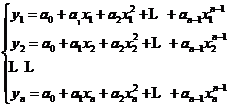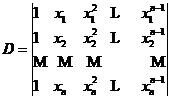剩余内容已隐藏，请支付后下载全文，论文总字数：10318字