论文总字数:8734字
目 录
0、引言 3
1、因式分解相关理论 3
1.1多项式的可约性 3
1.2特殊多项式的定义 3
1.3特殊多项式的性质 4
2、因式分解常见的几种方法 4
2.1应用公式法 4
2.2提取公因式法 4
2.3十字相乘法 5
2.4双十字相乘法 6
2.5拆项添项法 7
2.6换元法 7
2.7主元法 8
2.8求根分解法 9
2.9待定系数法 10
2.10利用单位根的性质 11
2.11重因式分离法 12
2.12利用矩阵的初等行变换分解法 12
2.13利用行列式分解法 13
2.14利用导数分解法 15
3、结束语 16
参考文献 17
致谢 18
多项式的因式分解
陈建春
,China
Abstract:Factorization is to decompose a polynomial to the form of several the most simple integral expression’s product.It is an identity transformation.It occupies a high position in the field of mathematics.We use it in elementary mathematics widely.In many mathematical problems,we will use it..Factorization has varied methods,flexible use and strong logic.If we can master these methods,it will be of great help for the future study of mathematics.This paper introduces several types of polynomial and various methods of factorization.These methods is from shallow to deep.They are explained through the examples to let everybody master these methods easily.
Key words:Factorization;Polynomial;Method of factorization.
0、引言
因式分解是指把一个多项式分解为几个最简整式的积的形式.在代数运算中,我们经常会运用到因式分解,它能化简代数式,帮助我们解决问题.因式分解是一种重要的恒等变换,灵活运用因式分解有助于我们解决各种代数式的问题.
因式分解包含了许多基础知识,它亦是中学数学中重要的学习内容,它对三角函数与解方程的学习很有帮助,有利于我们进一步的学习.但因式分解不仅仅只适用于中学的学习,在大学,我们依然可以运用,并且能接触到更深层的方法,所以我们更不能小觑了因式分解.
由于在进行因式分解的时候需要我们灵活的运用学过的数学基础的知识,并且因式分解的方法很广,技巧性也特别强,逆向思维具有一定的深广度,因此因式分解是发展学生智力、培养学习能力、深化学生逆向思维的良好工具.正因为因式分解具有培养学生学习能力和思维能力的功能,所以因式分解亦是中学代数学习中的一个难点,多项式因式分解是代数式中的重要内容,而多项式乘法的逆变形就是因式分解方法的理论依据,通过大学的专业知识学习,我们又接触到了更多且更有深度的因式分解方法,因此,让我们来了解并学习多项式因式分解的相关知识吧.
1、因式分解相关理论
1.1多项式的可约性
(1)在复数域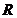 上,只有一次式是既约的,也就是说一个大于一次的多项式一定可以分解为几个一次因式的乘积.
上,只有一次式是既约的,也就是说一个大于一次的多项式一定可以分解为几个一次因式的乘积.
(2)在实数域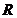 上,一次式和二次式(判别式
上,一次式和二次式(判别式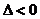 )是既约的,也就是一个多项式可以分解为几个一次因式和二次因式的乘积.
)是既约的,也就是一个多项式可以分解为几个一次因式和二次因式的乘积.

(3)在有理数域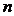 上,任意正整数次数的多项式都可以是既约的.
上,任意正整数次数的多项式都可以是既约的.
1.2特殊多项式的定义
①、对称多项式
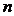 元多项式
元多项式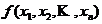 ,如果对于任意的
,如果对于任意的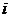 ,
,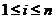 ,
,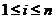 ,
,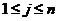 ,都有
,都有






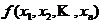 ,
,
那么这个多项式称为对称多项式.这就是说,任意对换两个字母的位置,原多项式恒不变,那么该多项式就是对称多项式.
②、轮换多项式
设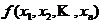 是
是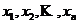 元多项式,如果将未知数
元多项式,如果将未知数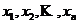 按照一定的顺序进行轮换,例如以
按照一定的顺序进行轮换,例如以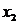 代
代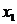 ,以
,以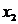 代
代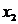 ,以
,以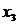 代
代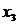
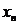 ,以
,以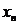 代
代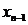 ,以
,以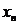 代
代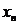 ,则有
,则有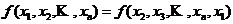 ,就称该多项式是轮换多项式.
,就称该多项式是轮换多项式.


③、交代多项式
如果一个多项式中将两个变数字母进行对换,结果原来的多项式只是改变了式子的符号,那么我们就称这个多项式为关于这两个变数字母的交代式.
1.3特殊多项式的性质
1.两个同变数对称式的和、差、积、商(能整除)是对称式.
2.两个同变数交代式的和、差是交代式,积、商(能整除)是对称式.
3.同变数的对称式与交代式的积、商(能整除)是交代式.
4.两个同变数的轮换式的和、差、积、商(能整除)是轮换式.
2、因式分解常见的几种方法
2.1应用公式法
如果你熟悉一些乘法公式,并能熟练的将它们反过来运用,就能将一些多项式因式分解,这种方法叫做公式法.常用的乘法公式如下:
完全平方式: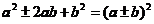 ;
;
平方差公式: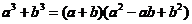 ;
;
立方和公式: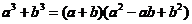 ;
;
立方差公式: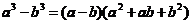 ;
;
完全立方式: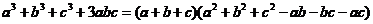 ;
;
其他公式: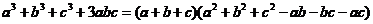 .
.
例1、将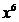 因式分解.
因式分解.
解:观察原题,我们发现只要将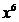 看作
看作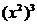 ,那么原式就满足立方和公式了,所以,
,那么原式就满足立方和公式了,所以,
原式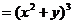 .
.
剩余内容已隐藏,请支付后下载全文,论文总字数:8734字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


