论文总字数:8844字
目 录
1、与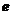 有关的极限问题 ...........................................4
有关的极限问题 ...........................................4
1.1 幂指函数的极限的求解 4
1.2 利用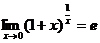 求解极限问题 5
求解极限问题 5
1.3 stirling公式在极限问题中的应用 8
1.4 利用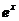 的展开式来求解极限问题 9
的展开式来求解极限问题 9
2、与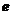 有关的级数问题 11
有关的级数问题 11
3、与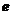 有关的积分问题 12
有关的积分问题 12
3.1伽马函数 12
3.2利用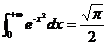 求解积分问题 13
求解积分问题 13
4、与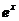 有关的指数函数问题 13
有关的指数函数问题 13
4.1 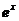 的妙用 13
的妙用 13
4.2 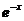 的妙用 14
的妙用 14
5、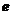 的估算和计算 14
的估算和计算 14
5.1 数列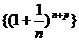 14
14
5.2 比较不同数列收敛到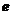 的速度 16
的速度 16
6、用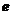 来刻画的特殊问题 18
来刻画的特殊问题 18
6.1 用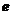 来刻画平均值之间的关系 18
来刻画平均值之间的关系 18
6.2 用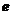 来刻画数列的极限问题 19
来刻画数列的极限问题 19
7、总结 21
参考文献 22
浅谈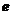 的认识与应用
的认识与应用
郭梦梦
,China
Abstract:This paper mainly explores the understanding and application of e in college mathematics.Firstly,the benefit of power exponential function,together with a special class of limits and Taylor expansion,is introduced in terms of solving limits.Then,according to limits, its implementation is generally applied for integral and series ,which brings some convenience in solving the problem.What’s more,the discussion of the estimation and calculation of e is followed.A complete theoretical proof method is used to explore the convergence rate of the three calculation methods.In the end,we depict a special kind of problem in view of e ’ uniqueness.We not only find that e is a key to connect arithmetic mean and geometric mean,but also discover that e plays an important role in the upper limit of the positive sequence.And we prove the existence of the lower bound.
Key words:limits ;Taylor expansion ; convergence rate; integral
0、引言[1]
当今社会中,数学作为科学和技术的有效工具,帮助人们收集整理信息、建立模型,进而解决问题,借助它来探究和发现社会各种现象.在人们日常生活中,数学语言和我们息息相关,可以说数学深入每一个人的内心.在研究 的问题上,
的问题上, 最先被德国著名数学家雅各.贝努利在探究复利问题时发现的.他在研究连续复利问题时,遇到求解
最先被德国著名数学家雅各.贝努利在探究复利问题时发现的.他在研究连续复利问题时,遇到求解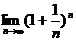 这个问题,他利用二项式定理,但因受当时数学发展的限制,求解出这个数介于
这个问题,他利用二项式定理,但因受当时数学发展的限制,求解出这个数介于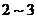 之间.
之间.
虽然贝努利是最先发现 的人,但最早使用字母
的人,但最早使用字母 命名的却是另外一位瑞士数学家—欧拉,符号
命名的却是另外一位瑞士数学家—欧拉,符号 首次公开出现在欧拉给数学家哥德巴赫的一封信中.后来欧拉在连分数的基础上,证明了
首次公开出现在欧拉给数学家哥德巴赫的一封信中.后来欧拉在连分数的基础上,证明了 是一个无理数,因此他才被认为是第一个指出
是一个无理数,因此他才被认为是第一个指出 是无理数的人,开辟了研究
是无理数的人,开辟了研究 的新纪元.
的新纪元.
 是数学中的重要常数之一.
是数学中的重要常数之一. 也是历史上第一个用极限来定义的数,本文先从极限部分指出,
也是历史上第一个用极限来定义的数,本文先从极限部分指出, 尤其在用幂指函数、一类特殊极限和泰勒展开的方法求解极限问题,发挥了举足轻重的地位.又详细介绍
尤其在用幂指函数、一类特殊极限和泰勒展开的方法求解极限问题,发挥了举足轻重的地位.又详细介绍 在求解极限方面带来的便利.积分和级数方面涉及的是无穷的问题.关于
在求解极限方面带来的便利.积分和级数方面涉及的是无穷的问题.关于 的级数通项和积分函数在计算中往往不易求解,专门研究
的级数通项和积分函数在计算中往往不易求解,专门研究 的积分和级数问题显得尤为必要.这里许多地方都是利用极限部分的知识来求解,就不再重复说明,本文主要针对其特殊之处加以说明.从
的积分和级数问题显得尤为必要.这里许多地方都是利用极限部分的知识来求解,就不再重复说明,本文主要针对其特殊之处加以说明.从 的发展过程来看,对
的发展过程来看,对 的估算和计算方面,一直是一个值得深入讨论的话题.收集和整理了多种关于
的估算和计算方面,一直是一个值得深入讨论的话题.收集和整理了多种关于 的估算方法,当然也有从概率论等其他角度出发的,本文主要探讨在数学分析中对
的估算方法,当然也有从概率论等其他角度出发的,本文主要探讨在数学分析中对 的估算方法,并用完备的理论证明,探究出
的估算方法,并用完备的理论证明,探究出 的三种估计方法的收敛速度.由于
的三种估计方法的收敛速度.由于 的独特性,在刻画的一类特殊问题中,
的独特性,在刻画的一类特殊问题中, 是连接算术平均值、几何平均值之间的桥梁,同时也是任意正数列上极限的下界[2].
是连接算术平均值、几何平均值之间的桥梁,同时也是任意正数列上极限的下界[2].
1、与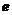 有关的极限问题
有关的极限问题
1.1幂指函数的极限的求解
我们将形式为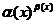 的函数,称为幂指函数,它的独特之处在于它既不能叫作幂函数也不能称为指数函数,正因为幂指函数的这种特性,使得它在求解极限的过程中变得十分复杂.从
的函数,称为幂指函数,它的独特之处在于它既不能叫作幂函数也不能称为指数函数,正因为幂指函数的这种特性,使得它在求解极限的过程中变得十分复杂.从 的独特性出发,得到几个有用的求解思路,使得幂指函数在求极限时化繁为简.
的独特性出发,得到几个有用的求解思路,使得幂指函数在求极限时化繁为简.
命题1.1.1[7] 当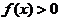 ,使得
,使得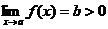 ,同时对于
,同时对于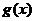 满足
满足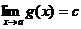 .则
.则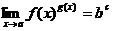 .
.
剩余内容已隐藏,请支付后下载全文,论文总字数:8844字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


