论文总字数:6066字
目 录
引言 3
1 凸函数的定义与基本性质 4
2 凸函数的一些扩充性质 5
3 凸函数理论在不等式证明中的应用 7
4 凸函数理论在积分极小值问题中的应用 10
5 几何凸函数的性质和应用 11
结论 12
参考文献 12
试谈凸函数理论的一些应用
郭俊
,China
Abstract:As one kind of important functions, convex function has been discussed simply in most textbooks of mathematical analysis. In this paper, we will make a further study of continuity and uniform continuity of convex function and its convexity of the integral average. Based on that, we summarize some skills of applications of the theories of convex function in inequalities. Also, we talk about how to prove Minkowski inequality, integral inequality and some other famous inequalities. We introduce the application of convex function in calculating extremum too. Last, we elaborate the properties and applications of geometric convex function as a supplement to the properties of convex function.
Key words:convex function;Holder inequality;extremum;geometric convex function
引言
凸函数是一类重要的函数,数学分析教材中已经作了初步讨论,让我们初步了解凸函数的一些理论及应用.本文进一步研究了凸函数的连续性、一致连续性及其在积分平均下的凸性.在此基础上,总结了凸函数理论在不等式中的应用技巧.在凸函数理论的一些应用中,我们知道的最多的应该是其在不等式证明中的应用.在很多不等式的证明中,我们经常遇到非常复杂的不等式证明,会给解答问题造成极其严重的影响,但我们知道凸函数与不等式之间存在着密切联系,这启发我们可以通过凸函数来证明不等式,使得问题更为简化.并且本文还探讨了凸函数在证明Minkowski不等式、积分不等式等一些著名不等式中的重要应用,也介绍了凸函数在求极值方面的一些应用并且给出了许多相应的例子.本文最后阐述了几何凸函数的性质与应用,充分展示凸函数在求几何问题里的重要作用.
1凸函数的定义与基本性质
定义1.1[3] 设函数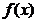 在开区间
在开区间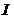 有定义,若对
有定义,若对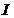 上任意两点
上任意两点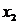 ,
,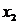 和任意实数
和任意实数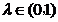 总有
总有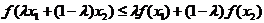 ,则称
,则称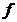 为
为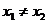 上的凸函数.若上式中
上的凸函数.若上式中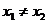 ,且不等号是严格不等号,则称
,且不等号是严格不等号,则称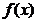 在区间
在区间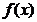 上是严格凸函数.若上述不等式中不等号反向,则称
上是严格凸函数.若上述不等式中不等号反向,则称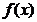 为
为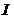 上的凹函数.
上的凹函数.
根据上述定义1.1可知,若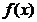 为区间
为区间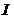 上的凹函数,则
上的凹函数,则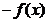 为区间
为区间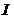 上的凸函数.因此只要研究凸函数,凹函数的性质可以由凸函数的性质推出.
上的凸函数.因此只要研究凸函数,凹函数的性质可以由凸函数的性质推出.
性质1.1[1] 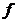 为区间
为区间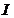 上的凸函数的充要条件是:对
上的凸函数的充要条件是:对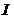 上的任意三点
上的任意三点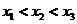 ,总有
,总有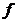 .
.
性质1.1的几何意义是: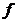 为凸函数的充要条件为在曲线
为凸函数的充要条件为在曲线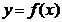 上从左到右任意三点
上从左到右任意三点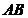 ,
,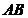 连线的斜率不大于
连线的斜率不大于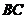 连线的斜率.
连线的斜率.
性质1.2[1] 令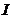 为
为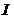 上的可导函数,则下列推断互相等价:
上的可导函数,则下列推断互相等价:
(1)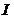 为
为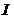 上的凸函数.
上的凸函数.
(2)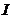 的导数为
的导数为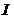 上的递增函数.
上的递增函数.
(3)对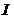 上的任意两点
上的任意两点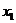 ,
,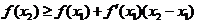 有
有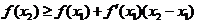 .
.
性质1.3[2] 若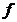 是
是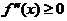 上的二阶可函数,则
上的二阶可函数,则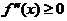 为其是凸函数的充要条件.
为其是凸函数的充要条件.
性质1.4[3] 令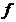 为
为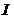 上的可导函数,则下列推断互相等价:
上的可导函数,则下列推断互相等价:
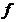 为
为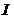 上的凹函数.
上的凹函数.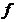 的导数为
的导数为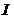 上的递减函数.
上的递减函数.- 对
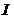 上的任意两点
上的任意两点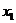 ,
,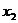 有
有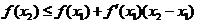 .
.
性质1.5[3] 若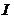 是
是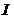 上的二阶可导函数.则
上的二阶可导函数.则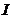 是
是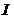 上凹函数的充要条件是:
上凹函数的充要条件是: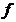 .
.
性质1.6 若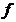 是区间
是区间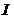 上的凸函数,则有Jensen不等式成立.
上的凸函数,则有Jensen不等式成立.
剩余内容已隐藏,请支付后下载全文,论文总字数:6066字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


