论文总字数:9082字
目 录
中文摘要 …………………………………………………………………II
英文摘要 …………………………………………………………………III
引言 ………………………………………………………………………1
1. 数域P上的幂零矩阵…………………………………………………2
1.1幂零矩阵的判定……………………………………………………………………………2
1.2幂零矩阵的一些性质………………………………………………………………………4
1.3特殊域上的幂零矩阵………………………………………………………………………5
1.3.1二元域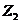 上的幂零矩阵…………………………………………………………5
上的幂零矩阵…………………………………………………………5
2. 整环上的幂零矩阵……………………………………………………7
2.1有限整环上的幂零矩阵……………………………………………………………………7
2.2无限整环上的幂零矩阵……………………………………………………………………9
2. 2.1整数环上的幂零矩阵……………………………………………………………9
2. 2.2整数多项式环上的幂零矩阵……………………………………………………10
3. 幂零矩阵的应用 ……………………………………………………11
参考文献…………………………………………………………………13
致谢………………………………………………………………………14
域和整环上的幂零矩阵
黄克顺
,China
Abstract: In this thesis, we study the nilpotent matrices over field P or an integral domain R. We give a necessary and sufficient condition for a matrix M over field P being nilpotent. We also show some properties for nilpotent matrices over integral domain R. In particular, we can give the concrete forms of the nilpotent matrices 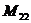 over the integers ring or the polynomial ring P[X], where P is a number field.
over the integers ring or the polynomial ring P[X], where P is a number field.
Keywords: field; integral domain; nilpotent matrix; residue class ring
引言
本文将要研究幂零矩阵,它是十分重要的矩阵,我们在矩阵的学习和研究中将会发现它的重要作用,许多问题都会借助其相关性质来解决. 文献[1]中主要研究了什么样的矩阵才是幂零矩阵,其中得到的主要结论有:矩阵为幂零矩阵,当且仅当矩阵的所有特征值均是0. 文献[2]给出了模n的剩余类环的重要性质以及一些基本定理,这些性质和定理对本文第二部分定理的证明有很大的帮助. 文献[3]研究了幂零矩阵经过运算后的幂零情况,得到的主要结论有:如果一个矩阵是幂零的,那么它的转置,伴随以及相似矩阵都为幂零的. 文献[4]针对二元域上矩阵进行研究,指出其幂零的条件并给出了一些重要的性质,得出重要结论:对于仅仅含元素1的矩阵,其中偶数阶的都是幂零的,而奇数阶的都不是幂零的. 文献[5]主要研究了幂零矩阵应用,用幂零矩阵的性质去证明一些问题. 而文献[6]-[11]主要涉及了幂零矩阵在高等代数和近世代数中的定义以及一些基本定理的证明和运用,这对本文的研究有很大的指导意义. 此外,对幂零矩阵判定也有一些研究,而且也获得了一系列数域P上幂零矩阵的结论. 而文献[12]-[15]主要是一些国外对幂零矩阵的研究成果,为我们的研究提供了很多的指导和启发.
我们在已有研究的基础之上进一步探讨了数域P上幂零矩阵以及整环上幂零矩阵应该具备的条件,得到有限整环上幂零矩阵的充要条件是当且仅当矩阵A的一切k阶主子式之和为零. 并且我们给出了幂零矩阵很多比较实用的性质以及相关的证明. 具体的讲,我们分别研究了三类数域:复数域、实数域和有理数域上的二阶、三阶的幂零矩阵的例子. 还运用幂零矩阵的相关性质去证明相关问题. 最后探讨了特殊数域--二元域上的矩阵是幂零的条件. 而在整环上幂零矩阵的探究中,我们研究了有限整环和无限整环的有关性质.
本文共分为三个部分. 第1部分,首先我们给出了整环、域以及幂零矩阵等后面会用到相对重要的概念的定义. 然后开始研究数域P上的幂零矩阵,得出结论:数域P上的矩阵A为幂零的充要条件是A的一切k阶主子式之和为零. 然后我们给出幂零矩阵一些重要性质. 当然我们还研究了二元域上的矩阵以及幂零的条件. 第2部分,我们得到有限整环R上的n阶矩阵A,若矩阵A为幂零的当且仅当矩阵A的一切k阶主子式之和为零. 并研究了模p的剩余类环的相关性质. 最后探究了整数环和多项式环上的二阶幂零矩阵的具体形式. 第3部分,对于幂零矩阵的应用,我们运用已证明的定理分别给出了有理数域、实数域和复数域上的二阶、三阶的幂零矩阵,并运用相应性质去解决有关问题.
1. 数域P上的幂零矩阵
1.1幂零矩阵的判定
为了便于研究数域和整环上的幂零矩阵,先给出数域、整环以及幂零矩阵的概念如下:
定义1.1: R为一整环,若有以下条件成立:
- 满足环的定义:设R为非空集合,R上定义的两种运算为加法和乘法,元
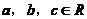
且1) R为加法交换群.
2) 乘法的结合律: 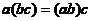 .
.
3) 乘法对加法的分配律: 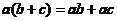
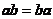
- 无零因子
- 乘法交换:
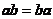
- 幺环:存在元素
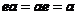 ,使得
,使得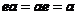 ,
,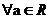 .
.
定义1.2:P为域,若有以下条件成立:
(1) P是交换的幺环
(2)P中至少含有两个元素
(3)而且全体的非零元素对乘法构成一群.
下面我们给出幂零矩阵的定义.
定义1.3:设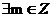 为数域P上的矩阵,如果
为数域P上的矩阵,如果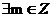 ,使得
,使得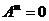 ,我们称
,我们称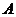 为幂零矩阵. 其中满足条件的
为幂零矩阵. 其中满足条件的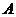 的最小值记作
的最小值记作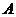 的幂零指数.
的幂零指数.
了解了幂零矩阵的概念后,下面我们将研究数域P上的矩阵为幂零矩阵应该具备的条件. 首先我们引入以下两个引理:
引理1.1 在数域P上,n阶矩阵
在数域P上,n阶矩阵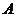 是幂零的,当且仅当矩阵
是幂零的,当且仅当矩阵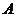 的所有特征值均是0.
的所有特征值均是0.
证明: 必要性: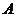 为数域P上的n阶矩阵,假设
为数域P上的n阶矩阵,假设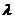 是
是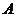 的任意特征值,对应的特征向量为
的任意特征值,对应的特征向量为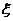 ,则有
,则有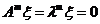 ,这里的
,这里的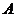 是矩阵
是矩阵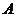 的幂零指数. 由于
的幂零指数. 由于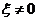 ,且
,且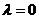 为正整数,于是得
为正整数,于是得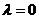 ,即幂零矩阵
,即幂零矩阵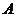 的任意特征根是
的任意特征根是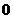 .
.
充分性:由题设知矩阵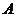 的所有特征值均是
的所有特征值均是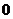 ,根据哈密尔顿-凯莱定理知
,根据哈密尔顿-凯莱定理知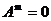 ,所以
,所以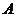 为幂零矩阵.
为幂零矩阵.
引理1.2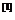 设数域P上的n阶矩阵
设数域P上的n阶矩阵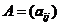 ,且它的特征多项式:
,且它的特征多项式: 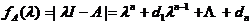 , 则
, 则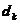 就等于
就等于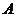 的所有
的所有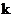 阶主子式的和乘以
阶主子式的和乘以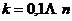 ,
,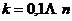 即
即
剩余内容已隐藏,请支付后下载全文,论文总字数:9082字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


