论文总字数:6778字
目 录
0引言 3
1. 预备知识与基本概念 3
2. 矩阵方程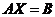 4
4
2.1矩阵方程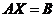 的解及性质 4
的解及性质 4
2.2矩阵方程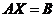 的解法 5
的解法 5
3矩阵方程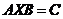 6
6
3.1矩阵方程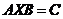 的解 6
的解 6
3.2矩阵方程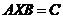 的性质 8
的性质 8
3.3数值例子 8
4. 矩阵方程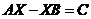 9
9
4.1矩阵方程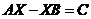 的解 9
的解 9
4.2矩阵方程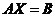 的性质 11
的性质 11
4.3数值例子 12
5.结束语 12
参考文献: 13
致谢 14
若干矩阵方程的解及性质
付琛
,China
Abstract:Matrix equation as matrix on the very important a branch, people had been very keen to study the matrix equation and method for solving the matrix equation has a lot of, also in addition to the important significance in the theoretical research, in remote sensing technology, theoretical physics, mechanical and electrical theory and technology, control theory and other fields have a very wide range of applications. AX=B are mainly discussed in the paper AXB=C and AX-XB=C, Kronecker matrix is used to study the several forms of matrix equation has solutions and the properties of the solutions. For algebra learning help.
Key words:Matrix equation; Kronecker product; Determination of solution.
0引言
矩阵本身的性质取决于元素的性质,最初矩阵是被当做工具来使用,在经历了近两个多世纪的发展后,现如今已成为单独的一门数学分支——矩阵论,同时矩阵论又可分为程论广义矩阵论,矩阵分解论,矩阵方程论等,并且现代理论矩阵及其理论也被广泛的应用于现代科技的各个领域之中。
矩阵方程作为矩阵论的十分重要的一个分支,人们一向很热衷于矩阵方程的研究,在查阅了很多资料文献之后,了解到矩阵方程的求解有很多,人们在不断的研究后又得出了一些新方法,在很多学报期刊中都有相关的文章发表,目前,矩阵求解问题在网络理论,数据分析,信号处理多元分析,现代控制理论,系统理论等(矩阵方程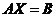 解的理论研究又可分为数值解法、解的唯一性、存在性、约束解等,而矩阵方程
解的理论研究又可分为数值解法、解的唯一性、存在性、约束解等,而矩阵方程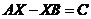 解的研究方向包括双对称解、对称解、相应的逼近解以及反对称解,另外矩阵方程
解的研究方向包括双对称解、对称解、相应的逼近解以及反对称解,另外矩阵方程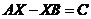 的研究也极为重要,例如:观测器设计、稳定性理论、极点配置都需要求解此类方程。)很多领域中都有着重要的应用,已成为代数学中非常重要的内容。
的研究也极为重要,例如:观测器设计、稳定性理论、极点配置都需要求解此类方程。)很多领域中都有着重要的应用,已成为代数学中非常重要的内容。
本文主要探讨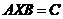 ,
,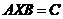 ,
,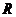 ,利用矩阵的kronecker积,研究这几种形式的矩阵方程有解的条件及解的性质,为以后代数学方面的学习提供帮助。
,利用矩阵的kronecker积,研究这几种形式的矩阵方程有解的条件及解的性质,为以后代数学方面的学习提供帮助。
所用记号如下: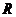 是实数域,
是实数域,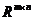 是
是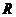 上的全体
上的全体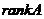 矩阵,
矩阵,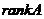 或
或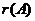 是矩阵
是矩阵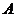 的秩,
的秩,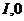 分别是适当阶数的单位矩阵和零矩阵,对于任意的
分别是适当阶数的单位矩阵和零矩阵,对于任意的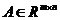 ,
,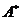 是
是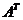 的共轭装置,
的共轭装置,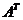 是
是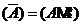 的装置,
的装置,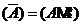
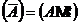 是矩阵方程的增广矩阵。
是矩阵方程的增广矩阵。
预备知识与基本概念
本节主要介绍矩阵的一些基本知识,首先介绍矩阵Kronecker积。
设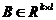 ,
,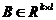 ,则称
,则称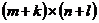 矩阵
矩阵
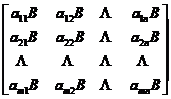
为矩阵A和B的Kronecker 乘积,记为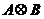 .
.
例如 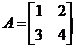 ,
,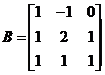 ,
,
则 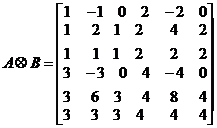 .
.
在研究的许多矩阵问题之中,Kronecker积都是极为有用的工具,大量的综合文献和书中都对矩阵的Kronecker积进行了详细的讨论。以下是矩阵Kronecker的基本性质,诸多文献都可以查到[5-7],综述如下:
设 为实数域
为实数域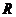 上满足运算的相应阶数矩阵,则
上满足运算的相应阶数矩阵,则
lt;1gt;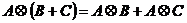 .
.
lt;2gt;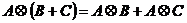 .
.
lt;3gt;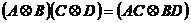 .
.
lt;4gt;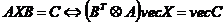 ,其中
,其中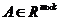 ,
,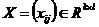 ,
,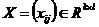 ,
,
那么有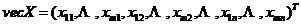 .
.
lt;5gt;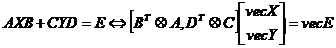 .
.
- 矩阵方程
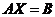
2.1矩阵方程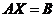 的解及性质
的解及性质
矩阵方程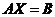 是常见的方程,许多文献[2-9]都做了详细的论述,高等代数(北京大学版)中讨论了该方程有解的充要条件及其求法,本节对此作出综述。
是常见的方程,许多文献[2-9]都做了详细的论述,高等代数(北京大学版)中讨论了该方程有解的充要条件及其求法,本节对此作出综述。
剩余内容已隐藏,请支付后下载全文,论文总字数:6778字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


