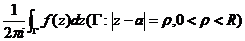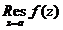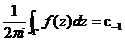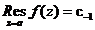留数定理的推广及其应用

论文总字数：6984字

目 录

1前言······································································································3

2留数定理······························································································3

2.1 留数的定义及求法················································································3

2.2留数定理及其求积分方面的应用································································4

3留数的推广························································································5

3。1 单个留数定理的推广···········································································5

3。2 对数留数定理的推广···········································································6

4留数的应用·······················································································8

4.1 级数求和的留数法···············································································8

4.2 在傅里叶级数展开中的应用·································································9

4.3 在物理问题中的应用············································································11

5结论································································································12

参考文献······························································································12

致谢·························································································14

留数定理及其应用

孔涛

，China

Abstract：Firstly，we introduce the residue and residue theorem，and give the method for solving the residue。Secondly，we extend the single residue theorem and the logarithmic residue theorem，some examples are also discussed。Finally，as the application of residue theorem，we discussed the problem of the summation of series，the expansion of Fourier series and the physical problems。

Key words：residue theorem；summation of series；the expansion of Fourier series；physical

1前言

1825年数学家Cauchy为了完善复积分理论而提出了一个重要的概念——留数。留数也叫作残数，是函数在其孤立奇点处的积分。之后，许多的数学研究者根据留数的性质对留数进行了很多的研究和推广，形成了一个相对完善的留数理论体系。同时应用留数定理可以对一些被积函数的原函数求不出来的积分进行求解。

留数定理有几种推广形式，例如李庆和林诗游在[1]中针对单个留数定理进行了一个推广，使外面的因式的幂指数等于右侧函数内的变量的指数加一。这个推广形式的留数定理能更加广泛的应用于积分的计算。戴振祥在[2]中将对数留数定理推广到任意多项式形式，更方便地通过解析函数的零点或极点来计算其留数值。

对于函数的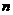阶极点处的留数计算公式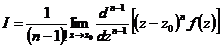，曹玉升在[3]中发现，式中的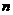只要是大于极点的阶数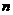，都是成立的。即当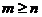时，函数在其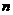阶极点处的留数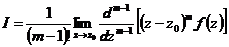。运用这个结论可以在计算留数的时候使计算过程简便许多。

对于留数的应用也不仅仅局限于求函数积分的问题，灵活运用留数可以解决很多问题，

例如在[4]中张毅对一种类型的实级数进行求和的时候就运用了留数定理，把问题转化为相关函数在其奇点处的留数和。计算矩阵函数值的时候，运用传统方法计算过程一般会非常复杂繁琐，刘芝秀在[5]中提供了计算矩阵函数值的留数法，通过文中所证明的定理将矩阵元素转化为可用留数定理计算的积分，然后得出矩阵的函数值。在[6]中，利用留数定理对函数进行傅里叶级数展开，在下面的论文中将给出具体方法。戴海峰在[7]中针对几种物理问题给出了运用留数定理的解题思路。

本文首先介绍了留数的定义和计算方法，还有柯西留数定理，给出了应用留数定理求解一些类型积分的方法；其次介绍了单个留数定理的推广形式及其证明，还给出了对数留数定理的一个推广。在应用方面，先给出了留数定理在级数求和方面的应用以及应用留数定理进行了傅里叶级数展开，最后还应用留数定理针对有阻尼振动的狄利克雷型积分进行了求解。

2留数定理

2.1 留数的定义及求法

定义1.1^[8]：假设函数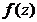以有限个点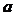为孤立奇点，可以解释为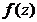在点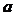的某去心领域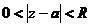内解析，那么称积分

为在点的留数，记为．

根据Cauchy积分定理可知，当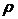的值满足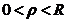时，留数的值与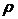没有关系，应用洛朗系数公式，

，

即

．

这时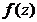在点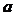处的洛朗展开式中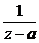项的系数就是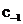，则函数在有限可去奇点处的留数为零。

根据上述留数的定义，我们可以利用孤立奇点的分类来求留数的值，具体方法如下：

设函数有孤立奇点，在点处的留数为，分情况讨论：

为函数在点处洛朗展开式负一次幂的系数

本质奇点

剩余内容已隐藏，请支付后下载全文，论文总字数：6984字