论文总字数:6680字
目 录
- 前言……………………………………………………………………4
- 压缩映射原理的推广…………………………………………………5
- 压缩映射原理的几个应用 …………………………………………10
3.1 ……………………………………………………………………………………………10
3.2 ……………………………………………………………………………………………10
3.3 ……………………………………………………………………………………………11
- 结论 …………………………………………………………………12
- 参考文献 ……………………………………………………………12
- 致谢 …………………………………………………………………13
压缩映射原理的推广及其应用
石健
, China
Abstract:In the paper, we first introduce the contractive mapping principle and some corollaries of the principle, then we extend the principle and give a more general fixed point theorem. Meanwhile, as the application of the principle, we study the limit of sequences, approximation calculation, solution of nonlinear equation, and some examples are also given.
Keywords:contractive mapping principle; generalized contractive mapping principle; limit of sequences; nonlinear equation; approximation
- 前言
波兰数学家Banach于1922年提出压缩映射原理。压缩映射原理在度量空间中有重要应用。确保了符合特定条件的自映射的不动点的存在性和唯一性。并给出了求不动点的具体方法。因此压缩映射原理也称为Banach不动点定理。数学分析中的极限和收敛等知识点都与压缩映射原理与有密切联系。随着人们对这一原理的深入理解,许多学者[1-3]对压缩映射原理做了一系列的推广,特别是[3]中给出了一个广义的Banach压缩映射。与此同时,压缩映射原理的使用领域也被进一步拓宽。例如敏志奇[4]利用压缩映射原理求递推数列的极限问题;铁勇[5]利用压缩映射原理处理高次线性方程,用以判断方程是否具有唯一解,并给出实根;张运章[6] 将压缩映射原理运用到图论中,分析了同地区不同比例地图的特点,并介绍了运用压缩映射原理解决积分方程的方法;张玲[7]将压缩映射原理应用到矩阵分析领域,对高阶矩阵的可逆性问题给出了较为简便的判定方法。受[4-7]的启发,本文将从两个方面来研究压缩映射原理:首先是对压缩映射原理进行推广;其次考察压缩映射原理在求解非线性方程,数列极限,近似值的计算等方面的应用。下面我们先给出一些已知的定义和结论。
定义1.1[8]:设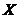 是一个非空集合,
是一个非空集合,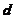 是
是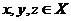 上的一个实函数,对所有
上的一个实函数,对所有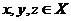 满足:
满足:
(i)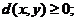
(ii)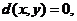 当且仅当
当且仅当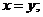
(ii)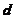 即三角不等式。
即三角不等式。
则称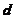 为
为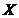 上的一个距离或者度量,此时
上的一个距离或者度量,此时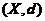 称为度量空间。若
称为度量空间。若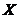 中每个点列都在
中每个点列都在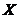 中收敛,则称
中收敛,则称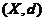 为完备度量空间。
为完备度量空间。
压缩映射原理讨论的对象是度量空间中的一类特殊映射,其定义如下:
定义1.2[6]:设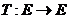 为一非空集,
为一非空集,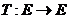 是一个映射,如果对
是一个映射,如果对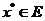 有
有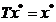 ,则称
,则称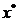 为映射
为映射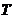 在
在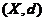 中的一个不动点。
中的一个不动点。
定义1.3[9]:设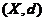 是一个度量空间,
是一个度量空间,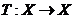 ,若
,若
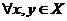 ,使得
,使得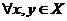 ,都有
,都有
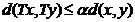 .
.
则称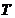 是一个压缩映射。
是一个压缩映射。
定理1.4[10](压缩映射原理):设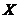 是一个完备度量空间,
是一个完备度量空间,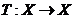 为一压缩映射,则
为一压缩映射,则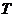 在
在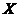 中有且仅有一个不动点。
中有且仅有一个不动点。
在文献[11]中,学者给出压缩映射原理的一个十分实用的推论。
推论1.5[11]:设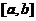 在
在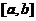 上连续,在
上连续,在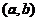 可微,且存在
可微,且存在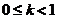 ,
,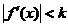 使得
使得
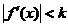
则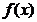 是
是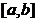 上的压缩映射。
上的压缩映射。
2、压缩映射原理的推广
定义2.1 :设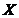 是完备度量空间,映射
是完备度量空间,映射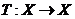 ,若
,若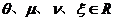
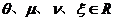 ,对
,对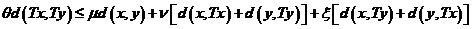 ,有
,有
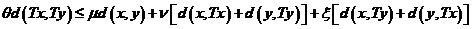 (2.1)
(2.1)
则称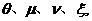 为一个广义压缩型映射。
为一个广义压缩型映射。
注:通过取特定的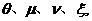 (2.1)定义的映射可转化为文[1-3]中推出的压缩型映射,特别地,当
(2.1)定义的映射可转化为文[1-3]中推出的压缩型映射,特别地,当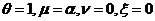 时,(2.1)即为定义1.3中的Banach压缩型映射;事实上,(2.1)定义的映射还包括了膨胀型映射。
时,(2.1)即为定义1.3中的Banach压缩型映射;事实上,(2.1)定义的映射还包括了膨胀型映射。
为了后面表述和论证的方便我们引入以下记号,对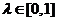 :
:
剩余内容已隐藏,请支付后下载全文,论文总字数:6680字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


