论文总字数:9049字
目 录
0.引言 4
1. 概念与引理 5
1.1 正交矩阵的定义 5
1.2正交矩阵的充要条件 5
1.3正交向量组 6
2. 正交矩阵的推广 9
2.1 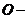 正交矩阵、
正交矩阵、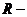 正交矩阵、
正交矩阵、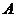 正交矩阵 9
正交矩阵 9
2.2 行正交矩阵与列正交矩阵 10
3. 正交矩阵的应用 12
3.1 正交矩阵在计算中的应用 12
3.2 正交矩阵在刚体运动中的应用 13
结语 16
参考文献 16
致 谢 17
正交矩阵的推广及其应用
刘悦倩
Abstract:Let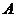 be a real square matrix. We call
be a real square matrix. We call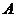 a orthogonal matrix if
a orthogonal matrix if 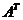 ,where
,where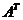 is the transposed matrix of
is the transposed matrix of 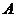 .We call
.We call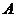 a
a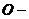 orthogonal matrix if
orthogonal matrix if 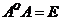 ,where
,where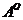 is the full transposed matrix of
is the full transposed matrix of 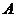 . We call
. We call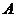 a row(column)-orthogonal matrix if
a row(column)-orthogonal matrix if 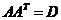 (
(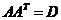 ),where
),where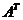 is the transposed matrix of
is the transposed matrix of 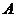 .In this paper we will discuss the properties of
.In this paper we will discuss the properties of 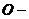 orthogonal matrices and row(column)-orthogonal matrices. Orthogonal matrices are important matrices, they have wide applications in mathematics and physics.We will discuss their applications in mathematical calculation and rigid motion.
orthogonal matrices and row(column)-orthogonal matrices. Orthogonal matrices are important matrices, they have wide applications in mathematics and physics.We will discuss their applications in mathematical calculation and rigid motion.
Key words:orthogonal matrix; 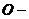 orthogonal matrix; row-orthogonal matrix;
orthogonal matrix; row-orthogonal matrix;
Column-orthogonal matrix.
0.引言
矩阵在数学领域中是一个重要的基本概念,是代数的主要研究对象之一,也是数学研究与应用的一个重要的基本工具.“矩阵”这个词是西尔维斯特第一个提出来的,他是为了将数字的矩形阵列区别于行列式而提出“矩阵"这个词的.
在矩阵论的发展史上,弗罗伯纽斯作出了突出贡献.他讨论了最小多项式问题,是第一个提出了矩阵的秩、不变因子和初等因子、正交矩阵、矩阵的相似变换、合同矩阵等概念的人,他不仅用逻辑的思维整理了不变因子与初等因子的理论,还在正交矩阵和合同矩阵这块领域上作出了巨大贡献.
在矩阵理论中,矩阵经常被用来描述变换.在实空间中正交变换,其度量是不会变的,由于正交矩阵是正交变换中所对应的变换矩阵,因此对正交矩阵的研究非常重要.矩阵的性质跟其元素的性质息息相关,矩阵在最初只是一种工具,但是经过两个多世纪的发展,现在已发展成为了一门独立的数学分支——矩阵论.
随着现在社会的进步和科技的迅速发展,高等代数这一门基础的工具学科不单单只在数学领域应用广泛,在其他领域的应用也数不胜数,它的作用越来越为世人所重视.因为矩阵是线性代数中的主要内容之一,并且正交矩阵又是一种常用的矩阵,所以越来越多的学者展开了正交矩阵在各个领域的研究.正交矩阵的研究不仅在外国遍地开花,在中国也百花齐放.例如:1981年赵英海发表了《砝码组合检定中正交矩阵的研究》,1990年李宏忠发表了《正交矩阵的法问题及其最佳逼近》,1999年温巧燕和肖国镇发表了《正交矩阵的递归生成算法》,2008年贾荷花发表了《正交矩阵分析法(PMF)大气颗粒物源解析技术的应用》.
本文在其他众多学者的研究基础上,对正交矩阵进一步进行推广与应用,推广到了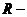 正交矩阵、
正交矩阵、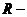 正交矩阵、
正交矩阵、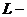 正交矩阵、行正交矩阵以及列正交矩阵.并讨论了正交矩阵在计算和刚体运动中的应用.尽自己卑微之力为正交矩阵这块领域的研究做出一定贡献.
正交矩阵、行正交矩阵以及列正交矩阵.并讨论了正交矩阵在计算和刚体运动中的应用.尽自己卑微之力为正交矩阵这块领域的研究做出一定贡献.
- 概念与引理
1.1 正交矩阵的定义
定义1.1.1[ 1]假设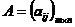 ,如果
,如果
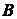 =
=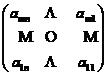 ,
,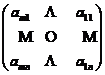 =
=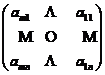 ,
,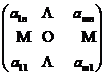 =
=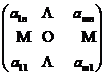
那么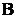 为
为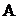 的全转置矩阵,用
的全转置矩阵,用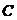 表示;
表示;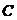 为
为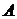 的右转置矩阵,用
的右转置矩阵,用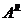 表示;
表示;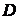 为
为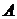 的左转置矩阵,用
的左转置矩阵,用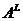 表示.
表示.
定义1.1.2[ 2]假设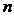 为
为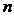 阶矩阵,如果
阶矩阵,如果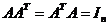 ,那么
,那么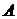 是正交矩阵.
是正交矩阵.
剩余内容已隐藏,请支付后下载全文,论文总字数:9049字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


