论文总字数:9116字
目 录
1导数在边际分析中的应用··································································3
1.1边际成本·······················································································4
1.2 边际收益··························································································4
1.3边际利润·····················································································4
1. 4 例题解析··························································································5
2导数在弹性分析中的应用································································6
2.1 弹性概念·······················································································6
2.2 经济弹性种类··················································································7
2.3 弹性分析·················································································8
2.4 例题解析·····················································································9
3导数在优化分析中的应用·······························································10
3.1 短期生产的合理决策·········································································10
3.2 例题解析·······················································································11
总结······································································································12
参考文献······························································································12
浅谈导数在经济学中的应用
姜炜
Abstract: Derivative plays a very important role in analysis of economic phenomenon. We summarize some applications of derivative in economics, embodies mainly in the marginal analysis and elastic analysis and optimization analysis of economics. We also elaborate the significance of these applications in economics analysis. Using the operation rule of derivative and image properties, we characterize the intrinsic relationship between the amount of economies quantitatively, and give a theoretical analysis of economic phenomenon in essentially.
Key words: Derivative;Marginal Function;Elasticity;Economics
在数学分析中微积分毫无疑问是一个重要的部分,其中微分学部分的基本概念由导数与微分组成.导数揭示了函数在瞬间变化的快慢程度.作为高等数学中的一个基本知识点,导数的应用已经渗透到了各个科技与文化领域当中,甚至也融入到人们的日常生活当中.
教材中对导数的概念给出了如下抽象定义(见[1]):设函数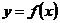 在点
在点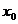 的某领域
的某领域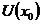 内有定义,
内有定义,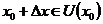 ,若是极限
,若是极限
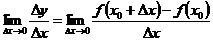
存在,则该极限形式就称为函数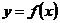 在
在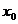 点的导数,记为
点的导数,记为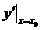 或
或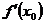 .
.
从数量关系上来看,导数反映的是函数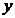 随自变量
随自变量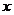 变化而瞬时变化的速度值.那么在解决实际的问题时,导数
变化而瞬时变化的速度值.那么在解决实际的问题时,导数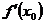 等于自变量
等于自变量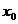 每改变一个单位量时函数
每改变一个单位量时函数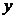 的改变量.这种思想恰恰符合经济学中的某些经济量的意义.
的改变量.这种思想恰恰符合经济学中的某些经济量的意义.
在经济领域中,我们可以运用导数的思想对实际的经济问题进行分析,利用导数工具来解决这些问题.导数应用十分显著的体现是经济学中的边际问题、弹性问题及优化问题.通常是在导数概念的基础上来对经济问题进行边际分析、弹性分析及优化分析,最后得出经济现象的定量刻画.研究导数在经济学中这些方面的应用,不仅丰富了导数的概念,也给初步掌握经济学基础知识的人带来了容易理解的简单快捷的计算方法.
本文总结了导数在边际分析、弹性分析及优化分析中的应用,利用导数定量刻画经济变量之间的内在联系,从本质上对经济现象进行理论分析.
1导数在边际分析中的应用
经济上把边际概念定义为经济变量的变化率,边际分析法则是依照导数的性质来研究某些经济变量的边际变化,在经济分析中十分常用.
对于边际经济变量的研究,西方的经济学家通常通过增加某一经济变量 单位观察另一经济变量因此变化了多少.显然,这就是导数在边际经济量上的体现(见[2]).一般的,经济学上把函数
单位观察另一经济变量因此变化了多少.显然,这就是导数在边际经济量上的体现(见[2]).一般的,经济学上把函数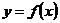 的一阶导数即
的一阶导数即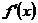 定义为该函数的边际函数,记为
定义为该函数的边际函数,记为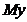 ,也即是
,也即是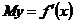 .相应地,
.相应地,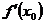 称为函数
称为函数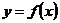 在
在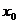 处的边际函数值,记为
处的边际函数值,记为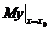 ,即
,即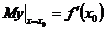 .
.
让我们用导数的意义来解释上述概念的含义,根据微分与导数关系,如果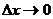 ,有
,有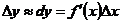 .不过在经济学中,
.不过在经济学中,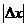 最小也有
最小也有 ,因为商品的增减量是不为
,因为商品的增减量是不为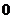 的.那么,当
的.那么,当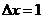 有
有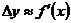 ,于是
,于是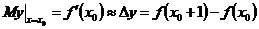 .也即是经济意义上的边际量表示为自变量为
.也即是经济意义上的边际量表示为自变量为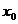 时再增加一单位,因变量
时再增加一单位,因变量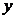 的改变量.
的改变量.
这充分地说明了边际概念就是把导数直接应用在经济学中而产生的.下面我们将细化地讨论具体的边际经济量是如何表现出导数的性质的.
剩余内容已隐藏,请支付后下载全文,论文总字数:9116字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


