论文总字数:6979字
目 录
中文摘要 II
英文摘要 III
引言 1
1 正定二次型 2
2 半正定二次型 3
3 负定二次型 7
4 半负定二次型 8
5 应用 11
参考文献 15
致谢 16
二次型及其应用
左嫣然
,China
Abstract:In this thesis,we focus on the judging positive semi-definite,negative definite and negative semi-definite quadratic forms.We show the judging theorems with complete proofs.Moreover,we give some applications of quadratic forms to the representation theory of algebras.
Key words:positive definite quadratic form;positive semi-definite quadratic form;negative definite quadratic form;negative semi-definite quadratic form
引言
正定二次型在高等代数中占有特殊的地位,也是线性代数的重要内容,它起源于几何学中二次曲线方程和二次曲面方程化为标准形问题的研究.二次型理论与域的特征有关.而在我们的教科书中,仅仅介绍了实二次型及其矩阵表示、正定二次型及其定义和简单性质,只涉及半正定二次型、负定二次型和半负定二次型的定义,而且对它们的性质研究的很少,只是在课本习题中零散地学习了一些相关知识.在大学学习中只能初步掌握相关知识,深刻、系统地掌握正定、半正定、负定和半负定二次型的性质及应用是很困难的.但根据对正定、半正定、负定和半负定二次型的重要作用及地位,所以有必要系统地研究讨论一下二次型及其应用的相关问题,本文先给出正定、半正定、负定和半负定二次型的定义,然后讨论了它们的若干性质.最后,利用它们的性质,讨论了许多关于它们的应用.
在查阅相关文献和书籍资料中,都只是简单介绍了正定二次型的定义和它的一些简单零散性质,也没有提及太多关于半正定、负定和半负定二次型的相关知识,对于它们的研究和应用也涉及不多.在文献[1]中正定二次型属于基础性知识,它有十分重要的地位,并且在解决实际数学问题中也应用广泛的.前人进行了一些有参考价值的相关研究,李秀英在文献[2]中根据负定二次型与半负定二次型的定义给出了它们的一些等价条件,并讨论了负定矩阵的一些性质.张淑娜等在文献[3]中根据正定二次型的定义给出了它的几个等价条件;并且通过对正定矩阵的考察,给出了正定矩阵的若干性质.魏慧敏在文献[4]中主要研究了二次型的一些判定定理判定及其应用,文献[5]和文献[6]分别对正定二次型的各个判定定理进行了系统证明.文献[7]- [15]的研究结果对论文的行文都有许多帮助.本文共分为五个部分.第1部分,对二次型的定义以及给出正定二次型的判定定理.第2部分,给出半正定二次型的定义及判定定理,并进行证明.第3部分,给出负定二次型的定义及判定定理,并进行证明.第4部分,给出半负定二次型的定义及判定定理,并进行证明.第5部分,我们将给出二次型在代数表示论中的应用.
1 正定二次型
为了研究二次型的性质,我们首先需要以下的例子和定义.
定义1.1 系数在数域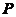 中二次齐次多项式
中二次齐次多项式
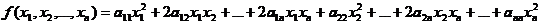 则它被称为数域
则它被称为数域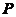 上的一个
上的一个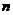 元二次型.其中
元二次型.其中
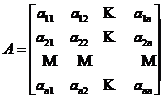 ,
,
满足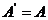 就称为二次型的矩阵,记
就称为二次型的矩阵,记
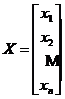 .
.
此时
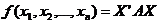 . (3)
. (3)
按上述的形式任意的一个方阵都可以组成一个二次型.
例1.1 二次型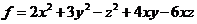 的矩阵为
的矩阵为
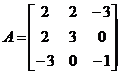 ,
,
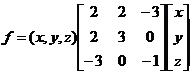 .定理1.1[1]
.定理1.1[1]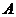 为数域
为数域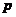 上的对称矩阵,
上的对称矩阵,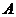 都与对角矩阵
都与对角矩阵 合同. 此时对角矩阵上1的个数
合同. 此时对角矩阵上1的个数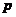 与-1的个数
与-1的个数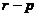 都是唯一确定的. 其中
都是唯一确定的. 其中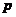 为矩阵的正惯性指数,
为矩阵的正惯性指数,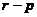 为矩阵的负惯性指数.
为矩阵的负惯性指数.
定义1.2[1] 如果对任何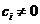 都有
都有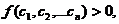 则称
则称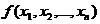 称为正定二次型. 二次型
称为正定二次型. 二次型
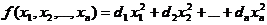
是正定的,当且仅当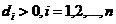 . 并称矩阵
. 并称矩阵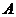 是正定的,记之
是正定的,记之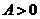 .
.
定理1.2 对于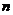 元实二次型,
元实二次型,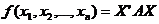 ,
,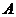 是其矩阵,其中下列条件等价:
是其矩阵,其中下列条件等价:
(1)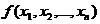 是正定的;
是正定的;
(2)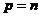 ;
;
(3)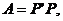 其中
其中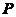 可逆;
可逆;
(4)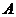 的顺序主子式全大于零;
的顺序主子式全大于零;
(5)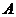 的特征值全大于零;
的特征值全大于零;
(6)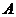 正定.
正定.
正定二次型定理的相关证明见文献[1].
2 半正定二次型在本节中我们主要研究半正定二次型的判定. 我们首先给出半正定二次型的定义.
定义2.1[1] 如果对于任意非零的实数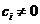 都有
都有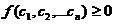 ,则称
,则称
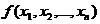
称为半正定二次型. 二次型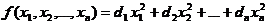 是半正定的,当且仅当
是半正定的,当且仅当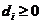 ,
,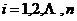 .
.
下面我们给出半正定二次型的判定定理.
定理2.1 设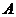 是
是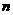 级实对称矩阵,对于实二次型
级实对称矩阵,对于实二次型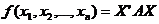 ,下列条件等价:
,下列条件等价:
(1)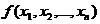 是半正定的;
是半正定的;
(2)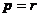 ;
;
(3)有可逆实矩阵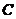 ,使
,使
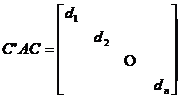 ,其中
,其中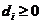 ,
,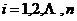 ;
;
(4)有实矩阵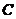 使
使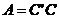 ;
;
剩余内容已隐藏,请支付后下载全文,论文总字数:6979字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


