论文总字数:8391字
目 录
1、引言 1
2、含参变量无穷限积分一致收敛性判别方法 1
2.1 定义法 1
2.2 Cauchy收敛原理 2
2.3 Weierstrass判别法 3
2.4 比较判别法 4
2.5 比较判别法的极限形式 5
2.6 对数判别法 5
2.7 Abel判别法 6
2.8 Dirichlet判别法 7
2.9 Heine定理判别法 8
2.10利用确界的方法 9
3、含参变量无穷限积分的性质 10
3.1 连续性 10
3.2 利用Dini定理判别收敛性 12
3.3 可微性 13
3.4 可积性 14
4、结束语 17
参考文献: 18
含参变量无穷限积分一致收敛性的判断及其应用
赵硕
,China
Abstract: This article summarizes some judging methods of the uniform convergence of parametric variable infinite integrals,for instance,Cauchy convergence criterion、Weierstrass criterion、Abel criterion、Dirichlet criterion and so on,by using the criterion of the uniform convergence of parametric variable infinite integrals.And the continuity and conductivity were also discussed based on the properties of the uniform convergence of parametric variable infinite integrals.
Keywords:Infinite integral with parameter variable;Uniform Convergence;Identification method; The property of infinite integral with parameter variable
1、引言
含参变量的无穷限积分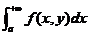 是数学分析课程的重要知识点,通过有效的判段含参变量无穷限积分是否一致收敛性对进一步研究含参变量无穷限积分的性质具有重要的意义,同时也可以为后继多元函数无穷积分学习打下坚实的基础,对数学的深入学习有着深远的意义和影响.然而,目前关于有关含参变量无穷限积分一致收敛性的判别方法在数学教材中提及的却并不多,且一些方法没有给出具体的证明过程和典型的例题,这对我们学习和研究含参变量无穷限积分产生了不小的难度.所以,本文在归纳总结了数学分析课本上的6种判别方法:一致收敛定义法、Cauchy收敛原理、Weierstrass判别法、Abel判别法、Dirichlet判别法、利用确界的方法.并且在此基础上提出了新的5种判别方法,即:比较判别法、比较判别法的极限形式、对数判别法、利用Dini定理判别收敛性、Heine定理判别法,并且给出了证明过程和典型的例子.
是数学分析课程的重要知识点,通过有效的判段含参变量无穷限积分是否一致收敛性对进一步研究含参变量无穷限积分的性质具有重要的意义,同时也可以为后继多元函数无穷积分学习打下坚实的基础,对数学的深入学习有着深远的意义和影响.然而,目前关于有关含参变量无穷限积分一致收敛性的判别方法在数学教材中提及的却并不多,且一些方法没有给出具体的证明过程和典型的例题,这对我们学习和研究含参变量无穷限积分产生了不小的难度.所以,本文在归纳总结了数学分析课本上的6种判别方法:一致收敛定义法、Cauchy收敛原理、Weierstrass判别法、Abel判别法、Dirichlet判别法、利用确界的方法.并且在此基础上提出了新的5种判别方法,即:比较判别法、比较判别法的极限形式、对数判别法、利用Dini定理判别收敛性、Heine定理判别法,并且给出了证明过程和典型的例子.
含参量无穷限积分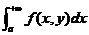 (其中
(其中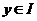 )对于参数的连续性、可积性都是在
)对于参数的连续性、可积性都是在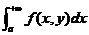 一致收敛的前提下得到的.而
一致收敛的前提下得到的.而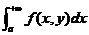 的可微性则需要
的可微性则需要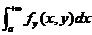 是一致收敛的.这在本文2.1、2.2、2.3的证明中得以体现.因此,有效的判别含参量无穷限积分的一致收敛性是极其重要的.
是一致收敛的.这在本文2.1、2.2、2.3的证明中得以体现.因此,有效的判别含参量无穷限积分的一致收敛性是极其重要的.
由于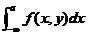 与
与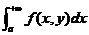 可以相互转化,而同样的可以通过参照
可以相互转化,而同样的可以通过参照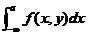 可以建立相应的
可以建立相应的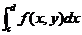 (
(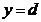 为函数的瑕点),从而判断其一致收敛性并讨论谈们的性质.所以本文只讨论了区间在
为函数的瑕点),从而判断其一致收敛性并讨论谈们的性质.所以本文只讨论了区间在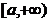 上的无穷区间,对于
上的无穷区间,对于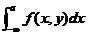 与
与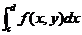 (
(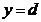 为函数的瑕点)的情况本文将不再累述.
为函数的瑕点)的情况本文将不再累述.
2、含参变量无穷限积分一致收敛性判别方法
2.1 定义法
定义2.1[5] 设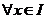 ,无穷积分
,无穷积分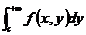 收敛,若
收敛,若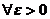 ,
,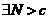 ,
,
当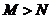 时,
时,
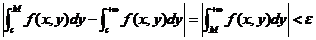 .
.
则称无穷限积分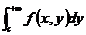 在区间
在区间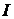 一致收敛.
一致收敛.
用定义法证明一致收敛的关键在于找到仅仅与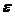 相关的
相关的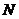 ,而方法一般是适当放大.
,而方法一般是适当放大.
定义2.2[5] 设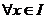 ,无穷限积分
,无穷限积分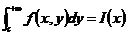 ,若
,若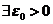 ,对
,对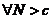 ,总存在
,总存在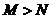 且
且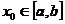 使得
使得
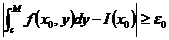
即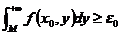 .则称无穷限积分
.则称无穷限积分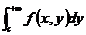 在
在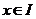 是非一致收敛的.
是非一致收敛的.
例 2.1 证明:无穷限积分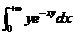 关于
关于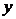 在区间
在区间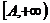 一致收敛
一致收敛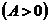 ,但在
,但在
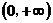 上不一致收敛.
上不一致收敛.
证明: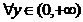 ,令
,令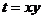 ,则
,则
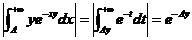 ,
,
对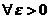 ,有
,有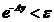 ,则
,则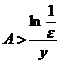 ,取
,取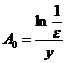 ,则
,则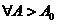 ,有
,有
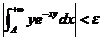 ,
,
所以,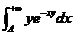 在
在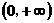 是一致收敛的.
是一致收敛的.
取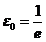 ,
,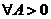 ,取
,取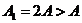 ,
,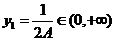 ,则
,则
剩余内容已隐藏,请支付后下载全文,论文总字数:8391字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


