论文总字数:9482字
目 录
1、引言 3
2、从不一致连续来看一致连续 3
3、一致连续性判定 4
3.1 利用定义 4
3.2 利用康托定理 6
3.3 利用导函数有界 9
3.4 利用函数的周期性 10
3.5 利用比值判别法 12
3.6 利用代数运算判定法 13
4、结束语 15
参考文献 15
致谢 17
函数一致连续性的判定和应用
夷志荣
,China
Abstract: Function of uniform continuity is the key content of mathematical analysis, is also the difficulty of its content. As we all know, the function continuity problem discussed is the function of local property, uniform continuity and function concept is the function of bearing the global properties. Function, therefore, uniform continuity problem research has important theoretical significance. This thesis mainly discuss the function of uniform continuity of several common methods and its application. Thesis is divided into four parts, including the first part is introduction, mainly introduction function the main result of uniform continuity, and have to expand the content of this article. The second part mainly through the constructor non uniform continuity of examples to deepen the understanding of the concept of uniformly continuous function. The third part mainly is uniformly continuity of function judgement, it is divided into six small, respectively using judgement of definition, judgement of cantor theorem, to judge and derived function boundedness with function of periodic decision, judgement of use ratio, using algebraic operation decision, etc. The fourth part is the conclusion, it is a summary of front several parts.
Key words: function; continuity; uniform continuity
1、引言
随着数学与其它科学的日益发展,是以关于函数性质的应用也越来越多,函数的一致连续性是在使用连续函数的过程中发展起来的一个概念.本文通过对函数一致连续性的概念、判别方法进行较为系统和全面的说明,并给出几种证明函数一致连续性的方法,同时也探讨了其相应的应用.
其实,判断函数的一致连续性的方法总结起来大概有六种主要的方法,分别为用定义判定、用康托定理判定、用导函数有界来判定、用函数的周期性判定、用比值判定、用代数运算判定.我们用的最多的是定义判断法,此方法是利用了函数一致连续性的定义:对任给的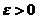 ,存在
,存在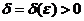 ,使得对于
,使得对于 ,只要
,只要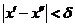 ,就有
,就有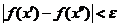 .则称函数
.则称函数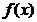 在区间
在区间 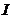 上一致连续,很多问题我们都可以通过这种方法来解决,但是这种方法解决某些问题可能不是那么方便,那么我们就需要通过其它的一些方法.例如,如果碰到一个定义在闭区间上的函数,我们可以尝试运用康托定理:假如一个函数定义在闭区间上,并且在这个区间上连续,那么这个函数在这个闭区间上一定一致连续.当然如果碰到一种函数利用定义不好解决,并且不是定义在闭区间上,我们可以就通过导函数有界:区间上可导且有界的函数必然一致连续来判断函数是否一致连续来证明,我们还可以通过判断函数是否一致连续来判断函数是否是周期函数,当然这需要用到函数的周期性:如果一个连续函数是具有周期性的,那么它必然是一致连续的,当然还有一些比较巧妙的方法,例如,通过构造一个函数
上一致连续,很多问题我们都可以通过这种方法来解决,但是这种方法解决某些问题可能不是那么方便,那么我们就需要通过其它的一些方法.例如,如果碰到一个定义在闭区间上的函数,我们可以尝试运用康托定理:假如一个函数定义在闭区间上,并且在这个区间上连续,那么这个函数在这个闭区间上一定一致连续.当然如果碰到一种函数利用定义不好解决,并且不是定义在闭区间上,我们可以就通过导函数有界:区间上可导且有界的函数必然一致连续来判断函数是否一致连续来证明,我们还可以通过判断函数是否一致连续来判断函数是否是周期函数,当然这需要用到函数的周期性:如果一个连续函数是具有周期性的,那么它必然是一致连续的,当然还有一些比较巧妙的方法,例如,通过构造一个函数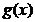 ,此函数和原函数
,此函数和原函数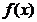 满足:⑴
满足:⑴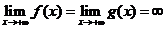 ;⑵
;⑵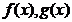 在
在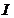 上可导,且
上可导,且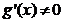 ;⑶
;⑶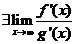 ,如果
,如果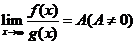 ,则
,则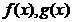 具有相同的一致连续性.这就是比值判定法,这样我们就可以通过判断
具有相同的一致连续性.这就是比值判定法,这样我们就可以通过判断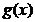 的一致连续性来得到
的一致连续性来得到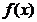 的一致连续性,其实当我们碰到某些函数可以分解为有穷个函数时,我们就可以通过代数运算判别法:有穷个一致连续函数的和必然是一致连续的,有限区间内,有穷个一致连续函数的乘积必然是一致连续的来判断函数是否一致连续.
的一致连续性,其实当我们碰到某些函数可以分解为有穷个函数时,我们就可以通过代数运算判别法:有穷个一致连续函数的和必然是一致连续的,有限区间内,有穷个一致连续函数的乘积必然是一致连续的来判断函数是否一致连续.
当然还有很多其它的方法,这里就不一一说明了.
2、从不一致连续来看一致连续
函数的一致连续性刻画了函数的连续程度.它表示的是函数的稳定程度.由此,我们可以给出不一致连续的定义.
定义[10]:设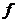 为定义在
为定义在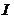 上的函数.假设
上的函数.假设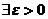 ,那么对于
,那么对于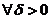 ,
,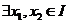 ,满足
,满足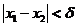 ,
,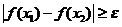 ,则称函数
,则称函数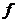 在
在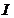 上不一致连续.
上不一致连续.
下面我们就给出几个不一致连续的例子以便大家更容易理解函数的一致连续.
例1:试证明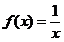 在区间
在区间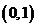 上连续但不一致连续.
上连续但不一致连续.
证明:令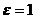 ,对于
,对于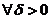 (此时我们不妨设
(此时我们不妨设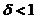 ),我们在区间
),我们在区间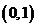 上取
上取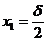 ,
,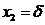 ,此时
,此时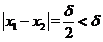 ,但是由于
,但是由于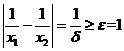 ,所以函数
,所以函数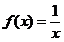 在区间
在区间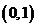 上连续但不一致连续.
上连续但不一致连续.
例2:试证明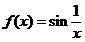 在区间
在区间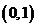 上连续但不一致连续.
上连续但不一致连续.
剩余内容已隐藏,请支付后下载全文,论文总字数:9482字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


