论文总字数:11445字
目 录
中文摘要..................................................................2
英文摘要..................................................................3
引言 1
1 整环上多项式的相关概念 2
1.1数域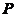 上多项式
上多项式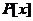 的性质 2
的性质 2
1.2整环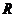 及其多项式环
及其多项式环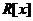 4
4
1.3唯一分解整环、主理想整环与欧几里德整环 5
2 整环上多项式满足带余除法 6
2.1整环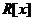 的带余除法定理 6
的带余除法定理 6
2.2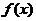 的根与因式形式 8
的根与因式形式 8
3 整环上多项式的因式分解 9
4 整环上多项式的最大公因式 11
4.1唯一分解整环上多项式环的最大公因式 12
4.2主理想整环上多项式环的最大公因式 13
4.3欧几里德整环的最大公因式 14
5 整环上多项式的重因式 15
参考文献 18
致谢.......................................................................19
整环上的多项式环理论
李梦
,China
Abstract: In this thesis, we study the polynomial ring theory in Integral Domain R.The following main results are obtained: (1) It is proved that the polynomial ring on the commutative ring satisfies the "remainder division" (with the first coefficient of the divisor a unit); (2) The polynomial ring in a unique factorization domain has a unique factorization; (3) The polynomial ring over a unique factorization domain has the greatest common factor; (4) For an arbitrary element f(x) in the polynomial ring R[x] over a unique factorization domain R, p(x) is f(x)’s k multiple divisor, then p(x) is the k-1 multiple factor of f(x)’s derivative.
Key words:integral domain; polynomial ring; unique factorization domain; greatest common factor; multiple divisor
引言
整环是抽象代数中的一个基本概念,在离散数学、计算机科学、物理学等学科中有很多的应用.聂灵沼、丁石孙[1]、刘绍学[2]等诸多学者对整环的整除概念有很多的研究,并且获得了一些重要结果[1].但是对于整环上多项式环理论没有进行系统的整理与探究.文献[1]提出了交换环都满足“带余除法”(当除式的首项系数为单位时)等整环的整除理论,提出了主理想整环和欧几里德整环,但并未将其进行多项式扩张.
文献[2]提出了Euclid算法,并由此推出分解的唯一性,且对整环的整除性质进行了研究.文献[3]主要是对于在数域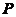 上多项式进行了研究,文献[4]给出了域与主理想整环的相关定理.文献[5]主要讨论了多项式的因式分解,着重在根和唯一分解整环上多项式的性质.文献[6]对各种特殊的整环进行了探讨.这些结果对我们研究整环上多项式理论奠定了扎实的基础.
上多项式进行了研究,文献[4]给出了域与主理想整环的相关定理.文献[5]主要讨论了多项式的因式分解,着重在根和唯一分解整环上多项式的性质.文献[6]对各种特殊的整环进行了探讨.这些结果对我们研究整环上多项式理论奠定了扎实的基础.
文献[7]~[15]也为文章的行文提供了很多的指导与启发.
本文共分为五个部分.第1部分,给出了数域上多项式的性质、整环上多项式及性质、三类重要整环(唯一分解整环、主理想整环、欧几里德整环)等概念.第2部分,给出整环上多项式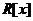 满足带余除法的定理及其证明,同时介绍根的性质.第3部分,首先给出反例说明整环上多项式一般不能满足唯一因式分解,其次引入唯一分解整环
满足带余除法的定理及其证明,同时介绍根的性质.第3部分,首先给出反例说明整环上多项式一般不能满足唯一因式分解,其次引入唯一分解整环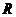 ,发现
,发现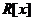 可以进行因式分解,并且满足高斯定理、艾森斯坦判别法,并由此得到一条关于根的性质.第4部分,对三类不同的整环进行研究,找出多项式环中任意两个元素的最大公因子.第5部分,介绍唯一分解整环
可以进行因式分解,并且满足高斯定理、艾森斯坦判别法,并由此得到一条关于根的性质.第4部分,对三类不同的整环进行研究,找出多项式环中任意两个元素的最大公因子.第5部分,介绍唯一分解整环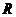 中,多项式环
中,多项式环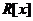 的重因式的性质,给出
的重因式的性质,给出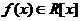 与导数
与导数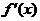 之间关于重因式的关系.
之间关于重因式的关系.
整环上多项式的相关概念
在本章中,我们将介绍数域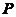 上的多项式概念和性质,并给出整环上多项式环概念.
上的多项式概念和性质,并给出整环上多项式环概念.
1.1数域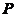 上多项式
上多项式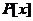 的性质
的性质
为了将数域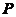 上的多项式理论推广到整环上多项式环理论,首先我们给出数域
上的多项式理论推广到整环上多项式环理论,首先我们给出数域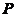 上的一元多项式相关定义.
上的一元多项式相关定义.
定义1.1[3] 我们称非空集合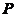 为数域,如果
为数域,如果
- 集合
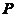 的元素皆为复数,且
的元素皆为复数,且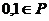 ;
; 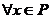 ,
,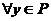 ,有
,有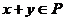 ,
,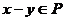 ,
,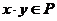 ,
,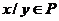 (此时
(此时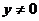 ).
).
再介绍数域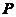 上的一元多项式的定义.
上的一元多项式的定义.
定义1.2[3] 对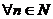 ,我们称表达式
,我们称表达式
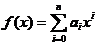
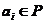
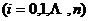 (1)
(1)
为在数域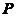 上的一元多项式.此时,在数域
上的一元多项式.此时,在数域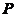 上的一元多项式的全体构成了环,记为
上的一元多项式的全体构成了环,记为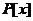 ,在此间,
,在此间,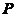 就是该一元多项式环
就是该一元多项式环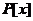 的系数域.
的系数域.
剩余内容已隐藏,请支付后下载全文,论文总字数:11445字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


