论文总字数:9444字
目 录
引言 1
1 线性空间和模上的相关概念 2
2 由线性空间推广到模论 7
2.1 线性空间和模的定义相似 7
2.2 线性空间中的线性表出与模上的线性组合 7
2.3 线性子空间与子模 8
2.4 线性空间上关于维数的定理与模同态基本定理 9
2.5 维数公式与模同态定理 10
2.6 子空间的直和与模的直和 11
2.7 可逆变换与模同构 11
3 无法由线性空间推广到模论的概念和定理 11
3.1 维数不能推广到模上 12
3.2 是否可以由基表出 12
3.3 线性空间上直和与模上外直和 12
3.4 同构判定定理不能推广到模上 13
参考文献 13
致 谢 14
从线性空间到模论
邓向东
,China
Abstract: Linear space and module theory are important conceptions in algebra.In this thesis, we first give the conceptions and theorems of linear space and module theory.Then we find the conceptions and theorems that corresponding to each other after analysis.Moreover, we find the conceptions and theorems that could not be extended from linear space to module theory and give counterexamples.
Key words:linear space; module theory; dimension formula; fundamental theorem of module homomorphism
引言
线性空间是高等代数中重要的研究对象.模论是近世代数里的基本内容,随着代数学的发展,线性空间和模的作用越来越重要,现在已经成为代数领域的重要研究工具.同时,线性空间和模论本身都是重要的研究对象.线性空间和模论存在许多相似的概念和定理,也有不同之处.因此,我们有必要将线性空间和模论上的概念和定理做出比较,找到它们之间的关系.
王萼芳、石明生[1]等学者对线性空间以及其上的重要概念和定理的做了很多研究,比如线性子空间及判定定理、维数公式、线性变换等,得到了许多重要结果[1].王尧、任艳丽[2]、聂灵沼、丁石孙[3]、张禾瑞[4]等学者模及其上的重要概念和定理进行很多研究,如模同态基本定理,模同构等,也得到了许多重要的结果[2][3].孙宗明[5]对维数公式与子空间直和的等价条件进行了深入研究.牛熠[6]研究了同态基本定理在向量空间中的应用,但是讨论的是环上的同态基本定理,具有局限性.这些学者的研究方向多是仅在线性空间或者是模上,并没有将它们统一联系起来.因此,为了更好地学习高等代数和近世代数以及找到高等代数和近世代数之间更深层的联系,我们需要做进一步的分析与研究.
本文通过线性空间与模论的对比,找出并证明可以由线性空间推广到模上的概念和定理,再找出哪些线性空间上的概念和定理不能推广到模上,并举出反例.
文献[1]给出了线性空间上的重要概念和公式以及部分重要定理的证明.文献[2]到[4]给出了模上的重要概念及部分重要定理的证明.文献[5]对维数公式以及子空间的直和进行了探讨.文献[6]讨论了同态基本定理在向量空间中的应用.
文献[7]到[16]也为文章的行文提供了许多指导与启发.
本文共分为3个部分.第1部分,给出线性空间和模的重要定义以及定理的概念.第2部分,通过对比,找出线性空间和模论中相互对应的概念,以及由线性空间推广到模论仍然成立的定理,如线性子空间对应子模、维数公式对应模同态定理、线性空间上的可逆变换对应模同构.第3部分,找出由线性空间推广到模论不成立的概念或定理并举出反例,比如维数、线性空间的同构判定定理,为了更直观地表达我们会举出反例进行说明.
1 线性空间和模上的相关概念
本章中,我们会给出线性空间和模上的基本概念.
首先,我们给出线性空间的定义.
定义1.1[1] 设有两个非空集,一个是集合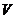 ,一个是数域
,一个是数域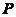 .在其上定义两种运算并满足下面的运算规律,则它们构成线性空间
.在其上定义两种运算并满足下面的运算规律,则它们构成线性空间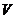 .
.
在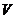 中定义运算,叫做加法,且对任意的
中定义运算,叫做加法,且对任意的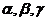
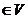 ,满足:
,满足:
- 加法封闭
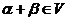 ;
; - 交换律
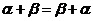 ;
; - 结合律
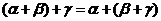
- 有零元 存在
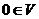 ,
,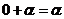 .
. - 有逆元 对于任意的
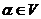 ,存在
,存在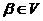 ,使得
,使得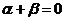 .
.
在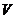 与
与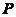 之间定义运算,叫做乘法,且对任意的
之间定义运算,叫做乘法,且对任意的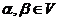 ,
,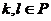 ,满足:
,满足:
- 封闭性
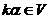 ;
; - 有单位元
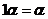 ;
; - 结合律
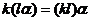 .
. 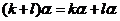 ;
;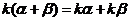 .
.
在分析有限维线性空间时,坐标是一个有力的工具,下面我们给出坐标的定义.
定义1.2[1] 设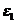 ,
,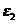 ,…,
,…,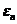 是
是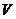 的一组基,
的一组基,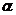
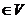 ,如果
,如果
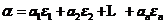
则称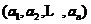 是
是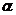 在基
在基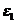 ,
,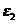 ,…,
,…,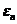 下的坐标.
下的坐标.
为了证明主要结果,下面我们定义线性子空间.
定义1.3[1] 设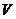 是数域
是数域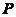 上的线性空间,且
上的线性空间,且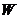 是
是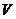 上的非空子集.如果
上的非空子集.如果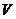 上的两种运算也可以使
上的两种运算也可以使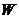 成为
成为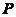 上的线性空间,就称
上的线性空间,就称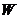 是
是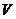 的线性子空间.
的线性子空间.
文献[1]中说明非空子集合成为子空间的条件.
剩余内容已隐藏,请支付后下载全文,论文总字数:9444字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


