论文总字数:7508字
目 录
O引言 4
1. Toeplitz矩阵的概念及性质 4
1.1 Toeplitz矩阵及其特殊形式的概念 4
1.2 Toeplitz三对角矩阵行列式计算 6
2. 三对角Toeplitz矩阵逆矩阵的求解 7
2.1 一般Toeplitz矩阵的逆矩阵求解 7
2.2 Toeplitz三对角矩阵的逆矩阵求解 9
3. Toeplitz三对角矩阵特征值和特征向量 11
3.1 求解Toeplitz三对角矩阵的特征值和特征向量 11
3.2 数值举例 13
4. Toeplitz三对角矩阵在图像处理中的应用 13
4.1 Toeplitz三对角矩阵在图像处理中的应用 13
5. 结束语 16
参考文献 16
致 谢 17
Toeplitz三对角矩阵的性质和应用
王妍
,China
Abstract: In practical production activities of dealing with the problems, the Toeplitz matrix is one of the most important tools.Toeplitz tridiagonal matrix is the widely used type of Toeplitz matrices. This paper introduces the concept and properties of Toeplitz matrices and its special form of matrix, discussing the Toeplitz tridiagonal matrix method for calculating the inverse matrix and the solution of the eigenvalue and eigenvector. In the term of application, we describe the Toeplitz tridiagonal matrices used in image processing.
Key words:Toeplitz three diagonal matrix; recursion; inverse; eigenvalue; Tikhonov regulation
O引言
在数学领域中,矩阵理论是十分重要的一部分,运用矩阵的理论和方法来描述一些复杂的问题,可以使其变得清晰简明。因而多年以来,矩阵在解决众多实际问题方面发挥了重要作用。其中,Toeplitz矩阵是矩阵类中被普遍使用的矩阵之一。
二十世纪初,德国数学家托普列茨第一次提出了Toeplitz矩阵的定义,并给出了一些关于它的简单性质。之后,众多学者又在此基础上对其进行分类并进行了深入的研究,例如,W.Eberly提出了关于带状类型矩阵的快速计算算法和一些基本性质。
Toeplitz矩阵的主要特点是主对角线上的各元素相等,平行于主对角线的各次对角线上元素也相等。该类矩阵在数学和工程中有着广泛的应用,而三对角类型的Toeplitz矩阵是就其中一类。在现实数据处理中,很多问题最终实质上是解Toeplitz三对角型线性方程组,而这类问题的求解重点就在于对Toeplitz三对角矩阵类型的系数矩阵的处理,所以,这类矩阵的性质一直作为研究重点为人们所关注。近年来,不仅在数值分析中出现大量有关Toeplitz三对角矩阵逆矩阵和该类型方程组的并行算法等的研究,而且在矩阵分析中,对Toeplitz三对角矩阵的特征值问题、幂的元素表达式等课题的研究也获得大量成果。
- Toeplitz矩阵的概念及性质
1.1 Toeplitz矩阵及其特殊形式的概念
定义1.1.1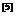 设
设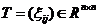 ,称矩阵
,称矩阵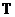 为Toeplitz矩阵,若矩阵元素满足
为Toeplitz矩阵,若矩阵元素满足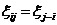 ,如
,如
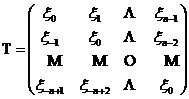 (1)
(1)
性质1.1.1 设 是Toeplitz矩阵,
是Toeplitz矩阵,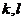 是任意实数,则
是任意实数,则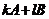 仍是Toeplitz矩阵。性质1.1.2 设矩阵
仍是Toeplitz矩阵。性质1.1.2 设矩阵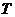 是Toeplitz矩阵,那么
是Toeplitz矩阵,那么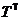 也是Toeplitz矩阵。
也是Toeplitz矩阵。
下面,我们可以通过广对称矩阵来说明Toeplitz矩阵的逆矩阵不再是Toeplitz矩阵。
定义1.1.2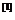 若
若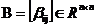 是广对称的,则它满足
是广对称的,则它满足
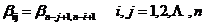
这等价于B满足
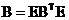
其中,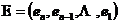 是n阶反序单位矩阵。由定义1.1.2,易证如果广对称矩阵可逆,其逆仍为广对称矩阵。
是n阶反序单位矩阵。由定义1.1.2,易证如果广对称矩阵可逆,其逆仍为广对称矩阵。
性质1.1.3 Toeplitz矩阵关于它的副对角线对称的,具有这样对称性的广对称阵矩阵称为广对角矩阵。由定义1.2知,Toeplitz矩阵的逆矩阵仍是广对称阵,但它不是Toeplitz矩阵。
Toeplitz矩阵关于它的副对角线对称的,具有这样对称性的广对称阵矩阵称为广对角矩阵。由定义1.2知,Toeplitz矩阵的逆矩阵仍是广对称阵,但它不是Toeplitz矩阵。
定义1.1.3
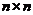 阶矩阵是Toeplitz矩阵
阶矩阵是Toeplitz矩阵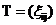 称为Toeplitz三对角矩阵,如果
称为Toeplitz三对角矩阵,如果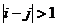 时,有
时,有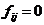 。形如
。形如
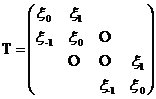 (2)
(2)
由元素的位置特点可以看出三个元素即可确定一个Toeplitz对角矩阵,所以,我们可以简单将(2)式记作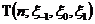 。
。
定义1.1.4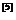 在(2)式中,若有
在(2)式中,若有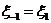 ,则称
,则称 为对称Toeplitz三对角矩阵,形如:
为对称Toeplitz三对角矩阵,形如:
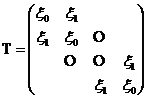 (3)
(3)
定义1.1.5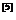
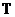 为循环Toeplitz三对角矩阵,若T形如:
为循环Toeplitz三对角矩阵,若T形如:
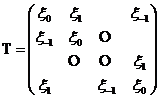 (4)
(4)
性质1.1.4 设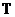 为循环Toeplitz三对角矩阵,那么
为循环Toeplitz三对角矩阵,那么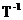 仍为循环Toeplitz三对角矩阵。
仍为循环Toeplitz三对角矩阵。
定义1.1.6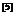 若当
若当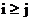 时,满足
时,满足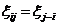 ,且
,且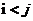 时,
时,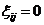 ,则称T为下三角Toeplitz矩阵,如
,则称T为下三角Toeplitz矩阵,如
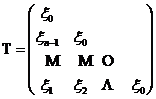 (5)
(5)
上三角Toeplitz矩阵定义与之类似,形如
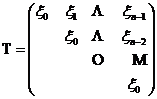 (6)
(6)
性质1.1.5 设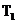 为下三角Toeplitz矩阵,那么
为下三角Toeplitz矩阵,那么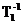 仍为下三角Toeplitz矩阵。上三角Toeplitz矩阵也有同样的性质。
仍为下三角Toeplitz矩阵。上三角Toeplitz矩阵也有同样的性质。
1.2 Toeplitz三对角矩阵行列式计算
剩余内容已隐藏,请支付后下载全文,论文总字数:7508字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


