论文总字数:7551字
目 录
1.引言 3
2.积分因子的基本概念 4
3.积分因子求法及其在解微分方程中的应用 4
3.1 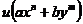 形式的积分因子求法及其在解微分方程中的应用 4
形式的积分因子求法及其在解微分方程中的应用 4
3.2 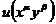 形式的积分因子求法及其在解微分方程中的应用 7
形式的积分因子求法及其在解微分方程中的应用 7
3.3 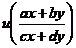 形式的积分因子求法及其在解微分方程中的应用 9
形式的积分因子求法及其在解微分方程中的应用 9
3.4 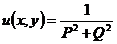 形式的积分因子求法及其在解微分方程中的应用 12
形式的积分因子求法及其在解微分方程中的应用 12
4.积分因子的其他应用 13
4.1 证明指数公式 13
4.2 证明对数公式 14
5.结束语 14
参考文献 15
致谢 16
积分因子方法及其在求解微分方程中的应用
刘晓萍
,China
Abstract:Total differential equations are a key part of differential equations.So the main innovation of this paper is to transform a non proper equation into a total differential equation. This process is very significant.The textbook is involved with integral factor concerning with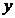 and with integral factor concerning with
and with integral factor concerning with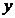 .This paper is mainly about other special integral factors which are proved.These conclusions will greatly improve the operational efficiency of solving differential equations,and lay a solid foundation for the study of other differential equations.At the end of this paper,it is proved that a kind of exponential formula and logarithmic formula.
.This paper is mainly about other special integral factors which are proved.These conclusions will greatly improve the operational efficiency of solving differential equations,and lay a solid foundation for the study of other differential equations.At the end of this paper,it is proved that a kind of exponential formula and logarithmic formula.
Key words:integral factor;total differential equation;original function;general solution
1.引言
由文[1] 知,假如对称式微分方程
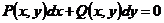 (1)
(1)
的左端是一个二元函数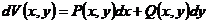 的全微分,即
的全微分,即
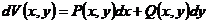 (2)
(2)
那么我们就称(1)式是全微分方程,为(1)的解,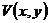 .而
.而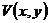 我们称为(2)式的原函数.
我们称为(2)式的原函数.
但是实际上并不是所有的微分方程都是全微分方程.下面给出了全微分方程的充要条件.
如果微分方程中的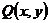 ,
,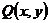 在如下矩阵区域
在如下矩阵区域
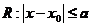 ,
,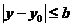
上连续可微,那么方程(1)是全微分的充要条件如下 在R上有
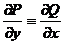 .
.
所以本文主要研究的就是把一个非恰当微分方程转变为全微分方程,这个过程具有很重要的意义.
常微分方程教材中只给出了如下两类特殊的积分因子
- 具有
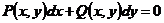 特殊因子的
特殊因子的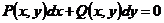 ,
,
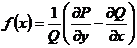 ,
,
容易求得积分因子为
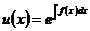 .
.
- 具有
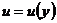 特殊因子的
特殊因子的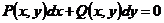 ,
,
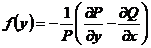 ,
,
容易求得而积分因子为
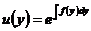 .
.
本文主要是这两类特殊积分因子的基础上进行拓展,探究了一系列其他的特殊积分因子,同时这也体现出本文的创新性,例如:只与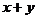 有关的积分因子、只与
有关的积分因子、只与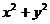 有关的积分因子、只与
有关的积分因子、只与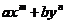 有关的积分因子、只与
有关的积分因子、只与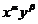 有关的积分因子、只与
有关的积分因子、只与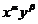 有关的积分因子、只与
有关的积分因子、只与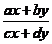 有关的积分因子、只与
有关的积分因子、只与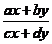 有关的积分因子和积分因子的形式是
有关的积分因子和积分因子的形式是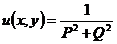 .本论文给出了以上八种特殊积分因子各自的证明方法以及例题.
.本论文给出了以上八种特殊积分因子各自的证明方法以及例题.
但是我们只要控制好含参数积分因子系数的变化,就可以把八种特殊积分因子简化为最基本的四种积分因子类型,分别是:积分因子只与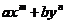 有关、只与
有关、只与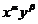 有关、只与
有关、只与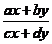 有关和积分因子的形式是
有关和积分因子的形式是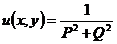 .当然还有很多其他类型的积分因子类型,由于字数有限,在此不一一列举.
.当然还有很多其他类型的积分因子类型,由于字数有限,在此不一一列举.
在本文最后我们还利用积分因子来证明对数公式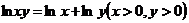 和指数公式
和指数公式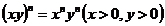 .
.
2.积分因子的基本概念
定义2.1[1] 如果存在这样的连续可微函数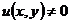 ,使方程
,使方程
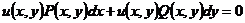 (3)
(3)
是全微分方程,则称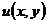 是微分方程(1)的一个积分因子。
是微分方程(1)的一个积分因子。
由上述积分因子的概念,我们可以得出全微分方程(3)的充要条件
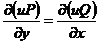 ,
,
展开上述方程得到
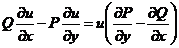 .
.
下面我们给出八种特殊积分因子的求法.
3.积分因子求法及其在解微分方程中的应用
剩余内容已隐藏,请支付后下载全文,论文总字数:7551字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


