仿射变换的性质及应用

论文总字数：8272字

目 录

0.1 摘要……………………………………………………………… 1

0.2 abstract………………………………………………………… 2

1 引言………………………………………………………………… 3

2 仿射变换在高等几何中的性质与举例…………………………… 3

2.1 仿射变换在高等几何当中的定义……………………………………………………… 3

2.2 仿射变换的性质………………………………………………………………………… 3

2.3 仿射变换的举例………………………………………………………………………… 3

3 仿射变换在初等几何当中的定义与性质………………………… 4

3.1 仿射变换在初等几何当中的定义与对比……………………………………………… 4

3.2 仿射变换的重要性质…………………………………………………………………… 5

3.3 利用代数表示的仿射变换……………………………………………………………… 5

4 仿射变换在平面几何之中的应用………………………………… 6

4.1 证明两个典型的仿射不变量的存在…………………………………………………… 6

4.2 利用仿射变换解决关于椭圆的问题…………………………………………………… 8

4.3 利用仿射变换解关于三角形的问题…………………………………………………… 10

参考文献……………………………………………………………… 11

致谢…………………………………………………………………… 12

仿射变换的性质与应用

曹正旸

Abstract：Firstly, the concept of affine transformation is defined by introducing the linear transformation plus the algebraic method, the plane intuition, etc. On this basis, the different definitions are compared.In the comparison process, some important properties of the affine transformations are obtained which mainly reveal the relevant affine invariant (line segment ratio, closed graph area ratio). Finally, we have combined on the affine transformation of knowledge, will be combined to the plane, to solve the problem on the cone curve, triangle and other issues So as to maximize the use of affine transformation of knowledge to solve those cumbersome secondary school geometric problems.

Key words: affine transformation ; affine invariant ;parallel projection

1 引言

在我们平常的生活中，数学已经逐渐成为了现代文化的一个极为重要的组成部分，之于我们平日的生活中，应用程度显得愈发频繁．而之于其他各个领域，数学是一个基本运行的基础，更是不断研究进步的必需途径．我们大学对于数学的学习与研究，就是让我们培养起一个良好的基础，能够使我们将之独立的应用于以后的工作和生活．

在我们大学学习中，仿射变换也许我们并没有给予特别多的关注，只是单纯的了解其知识点与定理．它只是在解析几何中提及过．但在这篇论文中，我想着重研究的就是仿射变换对于我们解题的利用以及在现实生活中的部分应用．

在这本文中，我们将基于解析几何的知识点，首先回顾其各角度的定义，了解其性质．对出现在几何中的题目举例分析．然后将其合理利用到初等平面几何之中，借之更方便快速的解决初高中几何问题．例如线段中点，椭圆的性质，三角形的中线、面积、线段，平行投影，仿射等价性，平行四边形及梯形的性质，不变点和不变线段，在已有基础上进行过了解与研究．

2 仿射变换在高等几何中的性质与举例

2.1 仿射变换在高等几何当中的定义

定义2.1.1 关于在两个向量空间之间，仿射变换是由一个可逆的线性变换再加上一个平移变换可以得到．即设T为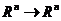在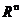上的线性变换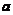，是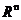上的一个向量，那么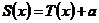,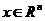成为在其上的仿射变换．

在几何中更直观讲，就是利用了线性变换与平移相结合，首先线性变换是符合了：第一点，变换前是直线的，变换后依然是直线不变，即保持了同素性（经过了非退化性的投影，点对应点，直线对应直线，曲线对应曲线）；第二点，线段的比例保持了不变；第三点，变换前对应的是原点，变换后它依旧是原点．即仿射变换．

2.2 仿射变换的性质

在进行仿射变换前后，两者保持

1. 同素性
2. 结合性（保持了点和直线之间的结合关系）
3. 共线性（向量的线性关系不变）

这三个性质不变．

2.3 仿射变换的举例

其中变换通过变换矩阵来实现举例．

1. 平移变换
   即保持变换前图形不变，进行空间位置上的位移．即将对应的每点移动到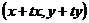，变换矩阵是．
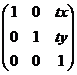2. 缩放变换

即保持了图形的整体不变，将其比例进行改变．将对应的横坐标放大或者缩小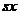倍，纵坐标放大或者缩小至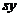倍，变换矩阵是．

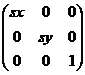1. 错切变换

即指图形沿着某方向产生了不等量的移动而引起的变换，变换矩阵是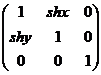，等同于一个横切变换和一个纵切变换的组合．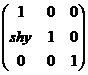

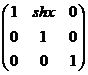1. 旋转变换

(i)目标绕着原点顺时针旋转了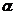，变换矩阵是．

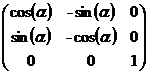(ii)目标以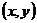为轴心顺时针旋转了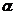，变换矩阵是

．

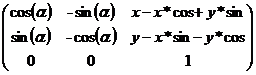3 仿射变换在初等几何当中的定义与性质

3.1 仿射变换在初等几何当中的定义与对比

定义3.1.1 平面上的点如果满足下面三个条件且是一一变换：

（1）任意在一条线上的三点的象仍然共线．

（2）任意共线三点之间的比例不变．

那么这个一一变换就可以称为仿射变换．

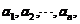
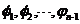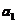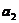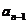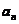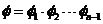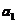定义3.1.2 假设在同一平面之中有n条直线依次为表示到，…到的透视仿射对应，使之建立了一一对应．而，如果与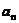重合，那么称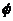为直线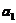到自身的仿射变换．

利用此定义，也可以借此定义在空间中的仿射变换，即将空间替代直线，通过空间中的点来建立一一对应．

剩余内容已隐藏，请支付后下载全文，论文总字数：8272字