论文总字数:3820字
目 录
1.引言 3
1.1母函数 3
1.2 Bernoulli数和Euler数 3
2.三角函数关系式与含有Bernoulli数,Euler数的恒等式 4
2.1考虑三角函数关系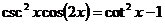 4
4
2.2考虑三角函数关系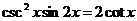 5
5
2.3考虑三角函数关系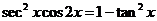 6
6
2.4考虑三角函数关系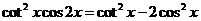 7
7
2.5考虑三角函数关系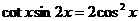 7
7
2.6考虑三角函数关系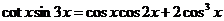 8
8
2.7考虑三角函数关系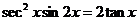 8
8
3.结论 9
4.讨论 9
参考文献 9
致谢 11
母函数与一些含有Bernouli数和Euler数的恒等式
储丹
,China
Abstract: Bernoulli number and Euler number have a relatively important position in combinatorial mathematics, number theory and theoretical physics. In this paper, by using the method of the mother function, some combination identities related to Bernoulli number and Euler number are established by using the power series expansion of some commonly used trigonometric functions.
Key words: generating function; Bernoulli number; Euler number
1.引言
1.1母函数
定义1 对任意的实数序列
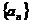 :
: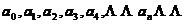 ,
, 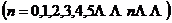
称形式幂级数
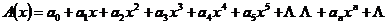
为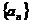 的母函数(或发生函数).序列
的母函数(或发生函数).序列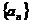 叫做母函数
叫做母函数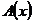 的生成序列.
的生成序列.
形式幂级数,就是在通常情况下, 把幂级数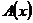 看作一个整体.在这里
看作一个整体.在这里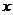 只是一个符号,不需要给它赋值, 因此在使用形式幂级时也不必要考虑它的敛散性.
只是一个符号,不需要给它赋值, 因此在使用形式幂级时也不必要考虑它的敛散性.
母函数方法, 就是在序列集合与形式幂级数集合之间建立一个映射,也就是说将难处理的序列问题转化为与之相对应的形式幂级数(母函数)来处理, 从而更容易地解决讨论的序列问题.
1.2 Bernoulli数和Euler数
对复数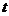 , Euler数和Bernoulli多项式分别由下面级数展开式定义
, Euler数和Bernoulli多项式分别由下面级数展开式定义
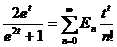 ,
, 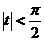
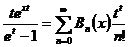 ,
, 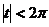
其中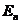 ,
,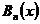 分别为Euler数和Bernoulli多项式,且
分别为Euler数和Bernoulli多项式,且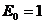 ,
,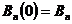 .
.
在数学文献中,Bernoulli数和Euler数在经典分析和数论中得到了广泛应用.
他们可以有以下两个三角函数的展开式
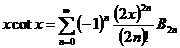 ,
, 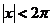 (1.2.1)
(1.2.1)
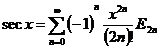 ,
, 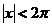 (1.2.2)
(1.2.2)
其中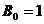 ,
,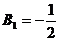 ,
,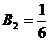 ,
,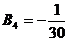 ,当
,当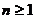 时,
时,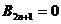 ,
,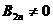 .
.
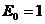 ,
,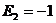 ,
,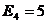 ,
,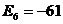 ,当
,当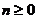 时,
时,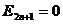 ,
,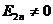 .
.
通过调用两个基本的三角关系
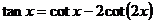 和
和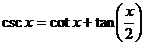 ,
,
我们不难得出另外两个含有Bernoulli数和Euler数的三角函数展开式
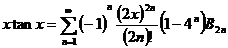 , (1.2.3)
, (1.2.3)
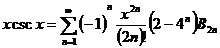 , (1.2.4)
, (1.2.4)
此外,下面是正弦和余弦函数的泰勒展开式
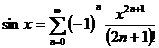 , (1.2.5)
, (1.2.5)
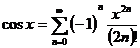 , (1.2.6)
, (1.2.6)
2010年Chu 等利用上述涉及到Bernoulli数,Euler数的展开式,进一步结合三角函数积化和差公式不仅推广了Liu
等利用上述涉及到Bernoulli数,Euler数的展开式,进一步结合三角函数积化和差公式不仅推广了Liu 的结果,还建立了若干新的等式,此方法简单实用,推导组合恒等式非常有效,受这篇文章启示,本文将寻找更多的三角函数关系,建立更多含有Bernoulli数和Euler数的组合恒等式.
的结果,还建立了若干新的等式,此方法简单实用,推导组合恒等式非常有效,受这篇文章启示,本文将寻找更多的三角函数关系,建立更多含有Bernoulli数和Euler数的组合恒等式.
2.三角函数关系式与含有Bernoulli数,Euler数的恒等式
2.1考虑三角函数关系
定理2.1 当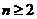 时,
时,
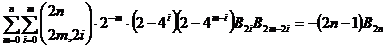 .
.
证明:在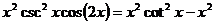 中带入展开式(1.2.1)(1.2.4)和(1.2.6),可以得到下列幂级数表达式
中带入展开式(1.2.1)(1.2.4)和(1.2.6),可以得到下列幂级数表达式
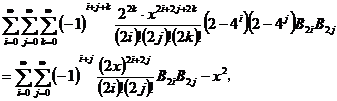
剩余内容已隐藏,请支付后下载全文,论文总字数:3820字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


