论文总字数:5068字
目 录
0、引言 3
1、二重积分的计算 3
1.1直角坐标系下二重积分的计算 3
1.2一般区域下的二重积分 4
1.3二重积分的变量计算 5
2、 三重积分的计算 7
2.1 一般区域下的三重积分 7
3、 重积分的应用 8
3.1 应用重积分求曲面面积 8
3.2 应用重积分求体积 8
3.3 应用重积分求薄片的质量 9
3.4 应用重积分求物体的质量 9
3.5 应用重积分求薄片的质心坐标 9
3.6 应用重积分求薄片的转动惯量 10
3.7应用重积分求物体的转动惯量 11
3.8 应用重积分证明部分广义积分 11
3.9 重积分在施工现场的应用 11
4、总结 13
参考文献 13
致谢 15
重积分的应用与计算
郭宇星
摘要:与单变量函数的积分类似,重积分拥有有以下性质(区域可加性,线性性质等).之所以通常情况下,求解重积分是将多重积分转换为单变量积分的组合,是由于每个单变量积分都能够解决的.
关键词:二重积分;三重积分;变量计算;
The application and calculation of multiple integral
Guo Yuxing
Abstract:Similar to the integral of a single variable function, the integral has the following properties (regional additivity, linear property, etc.). In general, the solution of the integral is to convert the multiple integral into a combination of a single variable integral, because each single variable integral can be solved..
Key words:double integral; triple integral; variable calculation;
0、引言
重积分是数学分析课程中主要的知识点,多元函数重积分的理论是类比一元函数定积分理论并将其推广得出的,最主要的差别就在于重积分的积分区域比一元函数的积分区间要复杂许多,这样就使得重积分在理论与计算上也要复杂一些.许多专家研讨的内容广泛而全面,实用性也是极高,这对我成功完成此次论文给予了很大的帮助,此篇文章将会重点探讨二、三重积分的定义和计算方法,以及重积分的应用.
1、二重积分的计算
1.1直角坐标系下二重积分的计算
定理1 设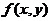 在矩形区域
在矩形区域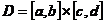 上可积,且对
上可积,且对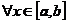 ,积分
,积分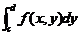 存在,则累次积分
存在,则累次积分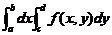 也存在,且
也存在,且
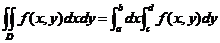 .
.
同理,设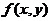 在矩形区域
在矩形区域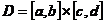 上可积,且对
上可积,且对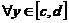 ,积分
,积分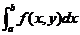 存在,则累次积分
存在,则累次积分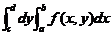 也存在,且
也存在,且
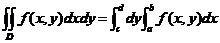 .
.
此外,若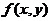 在矩形区域
在矩形区域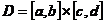 上连续,则
上连续,则
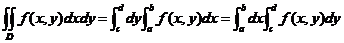 .
.
例1 计算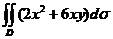 ,其中
,其中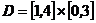 .
.
解 根据定理1有
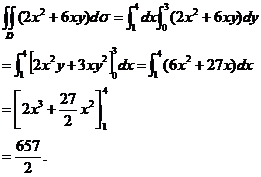
1.2一般区域下的二重积分
(1)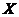 -型区域
-型区域
称平面点集
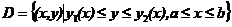
为 -型区域(图1).
-型区域(图1).
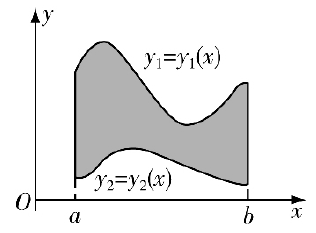
图1 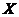 -型区域
-型区域
(2)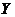 -型区域
-型区域
称平面点集
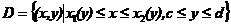
为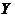 -型区域(图2).
-型区域(图2).
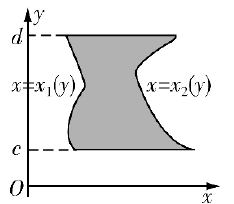
图2 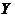 -型区域
-型区域
定理2 若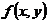 在
在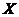 -型区域
-型区域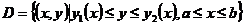 上连续,其中
上连续,其中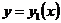 ,
,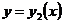 在闭区间
在闭区间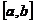 上连续,则
上连续,则
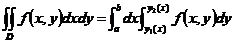
相似地,若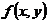 在
在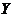 -型区域
-型区域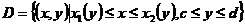 上连续,其中
上连续,其中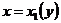 ,
,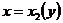 在闭区间
在闭区间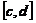 上连续,则
上连续,则
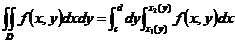
例2 求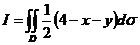 ,
,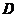 由直线
由直线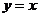 与抛物线
与抛物线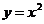 围成.
围成.
解 先画出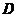 的草图(图3).
的草图(图3).
若选择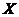 -型区域,则积分区域为
-型区域,则积分区域为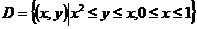 ,从而
,从而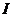 可化为:
可化为:
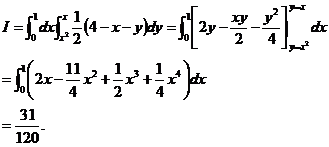
若选择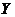 -型区域,则积分区域为
-型区域,则积分区域为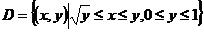 ,从而
,从而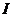 可化为:
可化为:
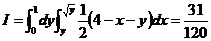 .
.
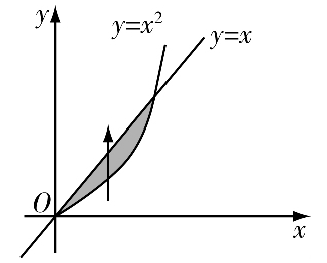
图3
1.3二重积分的变量计算
(一)二重积分的变量变换公式
引理 设变换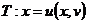 ,
,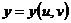 将
将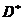 内的一个正方形
内的一个正方形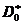 变换为
变换为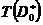 ,则
,则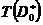 的面积为
的面积为
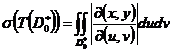 .
.
定理3 设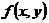 在
在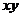 面上的有界闭域
面上的有界闭域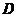 上可积,变换
上可积,变换
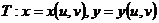
将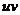 面上的有界闭域
面上的有界闭域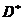 一一对应地变换为
一一对应地变换为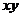 面上的有界闭域
面上的有界闭域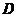 ,函数
,函数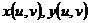 在
在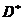 内分别具有一阶连续偏导数且
内分别具有一阶连续偏导数且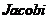 行列式
行列式
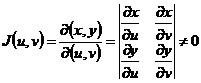
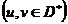 ,
,
则有
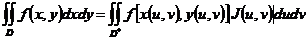 .
.
例3 求解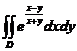 ,
,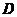 是被直线
是被直线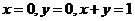 所围成的区域.
所围成的区域.
解 为了简化被积函数,令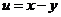 ,
,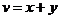 ,即作变换
,即作变换
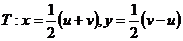 ,
,
剩余内容已隐藏,请支付后下载全文,论文总字数:5068字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


