空间曲线在平面上投影方程解法探讨

论文总字数：13956字

目 录

一、引言..................................................3

二、基本知识介绍..........................................3

2．1基本定义.............................................................3

2．2基本定理.............................................................4

三、空间中直线在平面上投影方法概述........................5

3．1空间中直线在坐标面上的投影方程.......................................5

3．2空间中直线在一般平面上的投影方程.....................................5

四、空间中曲线在平面上投影方法概述........................8

4．1空间一般式方程曲线在平面投影方程.....................................8

4．2空间参数式方程曲线在平面投影方程....................................10

4．3空间曲线在平面上投影的方法拓展......................................12

五、射影柱面的解法延伸...................................14

六、空间曲线投影应用的非典型例题.........................17

七、结论.................................................20

参考文献.................................................21

致谢.....................................................22

空间曲线在平面上投影方程解法探讨

郝晨辉

，China

Abstract: In spatial analytic geometry, the projection of the spatial curve on the plane is highly focused by researchers. We mainly discuss the solutions of spatial curve 's projection equation on the plane, we firstly summarize the methods of straight line's projection, secondly we learn the projection of the space curve in general equation and parametric equation and compare the differences, we also extend the elimination method so that it can be applied to the plane, finally, we sum up the methods of the projective cylinder and two atypical examples of application of space curve projection.

Key words: Space curve; Projective cylinder; Parameter equation

一、引言

解析几何与数学分析两门课程中，我们经常遇到求解空间曲线的各类问题．想要了解三维空间中曲线的各种性质，可以通过曲线在平面上的投影方程来学习．这类曲线投影问题也是空间解析几何中需要我们理解掌握的的重点与难点，重点在于曲线的平面投影可以帮助我们探索空间中曲线的形态，难点在于空间中的曲线是抽象的且形式及种类繁多，有时甚至无法想象出曲线的形状，但是可以从求解直线的投影入手，掌握一定的规律和技巧并将其应用于曲线投影的学习中．

空间曲线的表示方法通常有一般式方程和参数式方程两种，所以对应的解决方法有一般式法和参数式法两种，在对这两种方法进行学习时，已知解决这类问题的关键是求出投影柱面的方程，所以对射影柱面的解法进行深入探讨．在实际例题中，由于一些题目给出条件的特殊性，采用一般式方法并不是十分简便，这时可以将题中的特殊关系以及几何知识运用到解题中从而减少做题的复杂程度．

已知三维空间曲线在坐标面上的投影较为简单，且空间曲线与平面的相对位置不变，受到空间曲线在特殊坐标面上投影的解法，即消元法的启发，本文通过空间直角坐标的转轴变换将一般平面转化为坐标平面并用消元法求解，这样就使得消元法进一步应用于已知平面是一般平面的情况，为空间曲线在一般平面中的投影方程求解方法提供了新的思考方向．

二、基本知识介绍

详细地阅读文献[1]之后，我们对于空间几何的基本知识包括基本的定义和定理等内容做一个简单的回顾，这样方便后面学习不同解题方法时熟练运用几何知识，从而可以将各种方法灵活地运用到复杂的实际例题中．

2.1基本定义

定义1^[1]（向量的加法）：

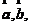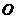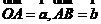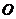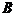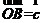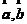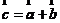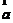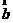已知两个向量以空间中任意一点为起始点作向量，得到一条折线，从折线的一端到另一端的向量，称为向量的和，记为．求两个向量与的和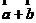，这样的运算称为向量的加法．

定义2^[1]（向量的外积）：

两个向量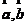的外积（也称为矢量积）是一个向量，记为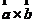或者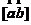，定义如下:

向量的方向为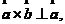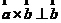，并且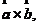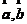符合右手法则，向量的模是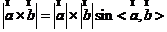．向量的外积也可以称为叉积或者是向量积．

定义3^[1]（平面束）：

在空间中经过同一条直线的所有平面组成的一个集合叫做有轴平面束，而这条直线称为平面束的轴．

定义4^[1]（空间直角坐标变换）：

空间中给出由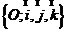和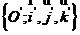标架决定的两个右手直角坐标系，分别称为新，旧坐标系，两右手标架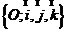和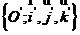的原点相同，即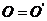，但坐标的基向量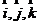与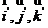不同，则新坐标系可看作旧坐标系绕着原点旋转，使得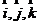与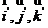重合，将这种情况的坐标变换称为转轴．其中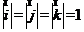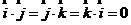，，并且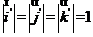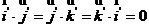，，所以空间直角坐标变换的转轴公式为

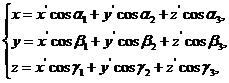
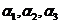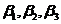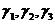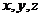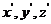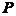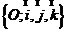其中，，分别是轴分别与轴之间的夹角，空间中任一点在和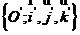下坐标分别为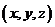和．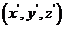

剩余内容已隐藏，请支付后下载全文，论文总字数：13956字