论文总字数：20459字

目 录

中文摘要．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．2

英文摘要．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3

引言 4

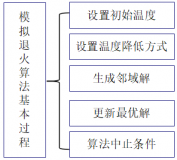
1 模拟退火算法基本思想 5

1.1局部搜索算法 5

1.2 固体退火过程与Metropolis算法 6

1.2.1固体退火过程的物理现象 6

1.2.2 Metropolis算法 6

1.2.3 Metropolis算法特性 7

1.3 模拟退火算法基本思想 8

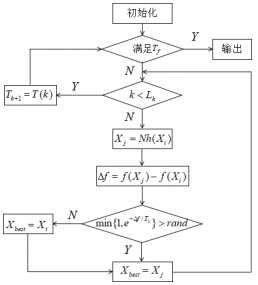
2 模拟退火算法基本步骤 9

2.1 算法符号说明 9

2.2 模拟退火算法基本步骤 10

2.3 温度参数降低方式、邻域函数与温度停止准则 11

2.3.1 温度参数降低方式 11

2.3.2 构造邻域函数 11

2.3.3 温度停止准则 13

3 模拟退火算法的渐进收敛性 14

4 模拟退火算法的实现 14

4.1 测试函数 14

4.2 编程实现 15

5 算法的缺点与改进 18

5.1 算法的缺点 18

5.2 算法的改进 18

5.3 改进后算法的实现 19

参考文献 19

致谢．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．21

附录．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．22

模拟退火算法在非线性函数优化中的应用

郜新宇

，China

Abstract: This essay is based on simulated annealing algorithm for global optimization of nonlinear functions. After studying the principle and basic steps of the algorithm, the global optimization of "Rastrigin" function and "Rosenbrock" function is realized by Matlab programming software. In the algorithm, a neighborhood function suitable for nonlinear continuous function is constructed, and a variable step size method based on the probability of new solution acceptance is introduced, which makes the global search from coarse to fine. Some defects of the traditional algorithm are improved. The improvement of the cooling method improves the accuracy of the algorithm and reduces the computational cost.

Key words：nonlinear function; global optimal; Simulated Annealing Algorithm; neighbourhood function; cooling method

引言

在处理实际工程中一些非凸目标函数的优化问题时，可能会出现多个极值的情况，则那些基于梯度的优化方法在沿着目标函数下降的方向搜索时，可能会因为“眼前的蝇头小利”而“固步自封、停滞不前”，最终导致搜索最优失败。所以我们希望采用一种具有跳出局部极值本领的全局优化算法来寻找问题的最优解。模拟退火算法（Simulated Annealing，简记为SA）作为一种具有算法描述简单、容易实现、运行效率高、初始条件限制弱等优点的优化算法，很好地满足了我们的要求。

模拟退火算法，顾名思义其主要思想模拟了固体的退火过程，起源于20世纪80年代初期，经过无数科研人员的改进与努力，其理论与应用已日益成熟。模拟退火算法应用最广泛的领域是组合优化问题，如旅行商问题（Travelling Salesman Problem，简记为TSP）、最大截问题（Max Cut Problem，简记为MCP）、调度问题（Scheduling Problem，简记为SCP）和图着色问题（Graph Colouring Problem，简记为GCP）（见文献[3]）但此算法的应用不仅仅局限于线性以及离散的优化问题，还可以应用于非线性目标函数的优化问题：文献[7]在传统算法的基础上，增加了记忆功能，并且设计了一个自适应的温度更新函数较少了计算量；文献[8]是针对高维非光滑非线性函数的约束优化问题；文献[9]、[10]都提出了适合非线性连续函数的邻域函数；这些参考文献总结的理论以及做出的创新让我们能够站在巨人的肩膀上看待问题，为我们的研究奠定了非常扎实的基础。文献[1]~[2]、文献[4]~[6]和文献[11]～[13]也为本文的行文和思路提供了很多的启发与指导。

本文将基于模拟退火算法对具有连续变量的非线性函数进行优化。本文一共分为五个部分：第1部分，给出关于模拟退火算法的一些基本思想及相关概念，主要介绍固体退火过程，Metropolis算法等。第2部分，介绍传统模拟退火算法的基本步骤以及算法中涉及到的参数的选取。第3部分，通过马尔科夫（Markov）链理论验证模拟退火算法的渐进收敛性。第4部分，通过一个连续型非线性函数优化的实例来实现模拟退火算法的应用。第5部分，陈述传统模拟退火算法存在的缺点，并针对这些缺点做出改进；最后再通过Matlab编程实现改进后的算法，并与传模拟退火统算法比较，得到了改进后算法能够提升精度且减少计算量的结果。

1模拟退火算法基本思想

在本章中，我们将介绍关于模拟退火算法的基本思想并给出一些必要的定义。

在介绍具体的算法之前，先确定需要解决的问题：通过模拟退火算法得到非线性函数的全局最优解。即

其中目标函数是一个（多元）非线性函数，是第i个约束条件，m是约束条件的个数，S是解空间。本文假定非线性函数的变量是连续型的，则上述优化问题又可以这样描述[1]：给定一组对偶，其中解空间为，而目标函数是映射，即从解空间映射到实数上的n维实函数，搜寻解空间中最小值点，使得对任意的，有

如果需要求解目标函数的最大值，则只要在目标函数前取符号即可，则问题可以转化为

1.1 局部搜索算法

局部搜索算法是一种简便灵活，且容易实现的搜索优化算法，它的基本思想是目标函数从某个初始解出发，然后在这个初始解的邻域内搜索，通常沿着目标函数梯度下降的方向（即）移动，且移动后继续搜索；否则返回当前解[2]。

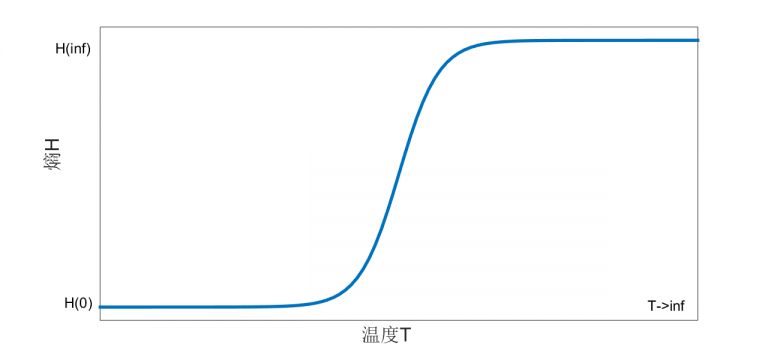
从局部搜索算法的基本思想不难发现它的局限性，正如同这个算法的名称一样，它只能在局部进行搜索。所以搜索结果的好坏很大程度上取决于初始解的位置，如果初始解位置在全局最优解附近则沿着梯度下降的方向很快就能找到“全局最优”；然而，如果初始解的位置远离全局最优解，则只能在初始解的邻域内勉强地用一个“局部最优”来代替这个“全局最优”了。以一个搜索一元非线性函数全局最小值为例（如图1所示）。

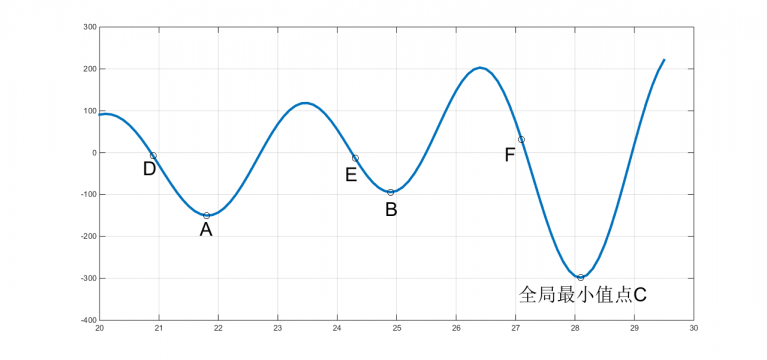图1 连续函数在其定义域内的极小值点

全局最优解在C处，而A,B两点都是局部最优解。如果初始解选择在F点处，则在F邻域内沿着梯度下降的方向定能搜索到全局最优解；如果初始解在D（或E）处，则在D（或E）邻域内沿着梯度下降的方向很可能会在A（或B）处就停止了搜索的步伐。

因此我们希望能克服搜索能力的局限性、脱离初始位置的限制，当遇到局部最优时，能够跳出这个“陷阱”。为此，我们首先引入固体退火过程以及Metropolis算法。

剩余内容已隐藏，请支付后下载全文，论文总字数：20459字

相关图片展示：