论文总字数：7722字

目 录

1、正交矩阵与广义正交矩阵的概念 3

1.1 正交矩阵的概念 3

1.2 广义正交的概念 3

1.3 广义正交矩阵的概念 4

2、正交矩阵与广义正交矩阵的性质及简单应用 4

3、利用正交矩阵求解特征值与优化迭代方法的收敛速度. 12

参考文献 16

致谢 18

附录 19

正交矩阵的性质及其应用

樊振铎

，China

Abstrcat: Matrix is an important basic concept in algebra，and orthogonal matrix plays an important 

role in advanced algebra,which is a kind of very special real square matix. And it has a pretty essential 

role in many aspects. In this paper we summarize some basic theorems on algebraic operations of 

orthogonal matrices and generalized orthogonal matrices.We discuss the inequalities derived from 

orthogonal matrices and their effects, and the applications of orthogonal matrices in optimized 

numerical calculation.

Keywords: orthogonal matrices，generalized orthogonal matrices, inequalities, Jacobi numerical 

calculation

1、正交矩阵与广义正交矩阵的概念

正交矩阵的概念

定义1.1^[1] 设阶实对称方阵，若（其中为阶单位阵，表示“矩阵的转置矩阵”）或（由下述结论2），则称阶实矩阵是一个正交矩阵.

若是一个正交矩阵，则显然可以得出如下结论：

1）：是正交矩阵；

2）：（为单位矩阵）；

3）：的各行是单位向量且两两正交；

4）：的各列是单位向量且两两正交；

5）：；

6）：的行列式为1或-1；

7）：.

广义正交的概念^[2]

基于正交的概念，我们有如下广义正交的概念：

定义1.2.1广义正交 设实对称矩阵以及两个维列向量、，若双线性型满足，此时称向量与是关于对称矩阵正交的.

定义1.2.2广义长度 设实对称正定阵以及维列向量，称为向量关于实对称正定阵的广义长度，特别的，定义广义长度为1的向量为关于该矩阵的规范化向量.

定义1.2.3规范化正交 设矩阵是实对称正定矩阵，和是两个维向量，若与分别关于正交，且与都是关于的规范化向量（即，），则称与关于规范化正交.

设向量，，和实对称正定矩阵

，

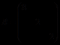则，，关于矩阵B正交，事实上，，，关于B规范化正交.

广义正交矩阵的概念^[2]

定义1.3.1广义特征向量 设有矩阵方程，并称为广义特征方程，由齐次线性方程组有解的充要条件（即系数行列式为0）推广易得矩阵方程有解的充要条件是上述方程成立，限于篇幅，推广证明过程略去.类似于普通的特征值与特征向量，该广义特征方程求解所得的根称为广义特征值，对应的非零向量称为广义特征向量.

定义1.3.2广义正交矩阵 设有阶实对称矩阵以及阶实对称正定阵，则由方程根据定义1.3.1求出的个线性无关的广义特征向量（事实上，必定会恰好有个互相线性无关的广义特征向量，由齐次线性方程组有解的充要条件这是显然的，否则会与方程组有解矛盾）所作=[,,...,]，其中，,,...,是关于规范化两两正交的维列向量，称为广义正交矩阵.

2、正交矩阵与广义正交矩阵的性质及简单应用

定理2.1^[4] 设与是两个阶实对称阵，其中是正定的，有个广义特征值，则必有一个广义正交矩阵同时满足：

剩余内容已隐藏，请支付后下载全文，论文总字数：7722字