论文总字数:10733字
目 录
1.引言……………………………………………………………………3
2.引入点估计方法………………………………………………………4
3.引入贝叶斯估计法……………………………………………………6
4.对于广义高斯估计的K-S检验法……………………………………9
5.矩估计的相合性判断 ………………………………………………10
6.估计方法的检验评价 ………………………………………………13
7.结论 …………………………………………………………………17
参考文献 ………………………………………………………………18
广义高斯分布参数估计探索
周杨程
,China
Abstract:Parameter estimation is a method for estimating unknown parameters in the total distribution based on samples taken form a population and plays an important role in probability theory,The generalized Gaussian distribution be used in adaptive detection and signal detection in many places. In this paper,, the properties of moment estimator satisfying the compatibility are verified.And in the case of a known,the Jeffreys transcendental model is introduced to estimate The Bayesian interval of the parameter β.At the end of the paper,the excellent properties of various estimators are compared by k-s method and analysis of sampling information.
Key word:Generalized Gaussian distribution;point estimation; k-s method; Bayesian estimate
1.引言
在经过很多的实验,文献[7]和[9]证实在图像小波系数方面高斯函数不能适用,但广义的高斯分布(GGD)却是一种应用在例如去躁等很多领域的先验分布。Mallat利用贝叶斯方法得到了有“coring”性质的估计量。并且,广义高斯分布也可运用于自适应检测和信号检测等很多领域,所以研究其参数估计是十分有意义的。
参数估计在模型的寻找建立运用非常广泛。大家往往通过取样样本信息,减小误差,去粗取精样本数据,然后通过分析,判段,通过对样本数据分析采用合适的统计量去推断总体的统计信息。统计推断是概率统计中相比于其他阶段更为关键的环节。统计推断的具体含义是通过观测值数据对研究对象的概率分布函数或统计信息正确的揣度。参数估计是一种十分基本实用的方法在统计推断中,是概率论和统计学的一个重要环节。参数估计的评估方法有很多,主要是无偏性,有效性,一致性,渐进性(随着样本数的增加满足的性质),最小方差无偏性等。其中无偏性是被广泛采用于对原估计方法判断合理性的一种性质。在文献[5]中介绍快速估计法很迅速,实质上就是为矩估计在k取值1,2时下的情形,运用函数拟合的方法来评价估计。本文末尾将判断在k取任意整数情况下矩估计是否满足渐进无偏性,来探讨矩估计在此方面的优良性。
贝叶斯估计是统计中的另一流派,在经典的学派中,往往通过总体和样本信息进行统计的推理和判断,贝叶斯学派认为还要加入先验信息(先验信息:试验,取样之前就已知的关于未知参数的一些统计概率信息),认为运用贝叶斯估计能够更加完善得对参数进行估计。然而Bayes估计的先验分布函数的择取是贝叶斯估计的十分复杂的部分,在很多场合非常困难。不同的先验分布得到的结果有好有坏,在文献[4]中详细得讨论了先验分布的选取。在本文中打算运用Jeffreys先验模型,当无先验信息或者先验信息很难挖掘的情况下,jeffreys方法是一个比较好的寻找先验分布的方法,也是十分广泛应用的先验模型。
在文献[9]-[15]在对估计评价方面给出了很多,但本文引入K-S检验,不需要先前知道数据的分布情况,可以算是一种非参数的检验。然而这样方便的代价是当数据服从特定的分布时,K-S检验的灵敏度没有相应的检验来得高。当样本较小时,KS检验在分析两组数据之间是否不同时十分常用。最后通过matlab将估计方法得到的数值对比,具体详见下文。
2.引入点估计方法
2.1 广义高斯分布密度函数:
 (2.0)
(2.0)

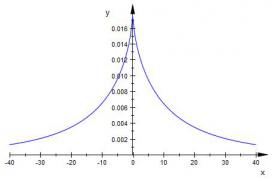
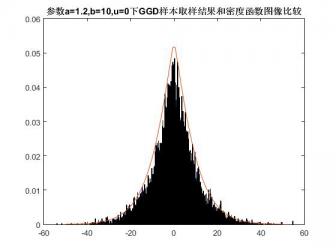
由于参数α影响控制广义高斯分布的衰减快慢,因而通常称之为‘衰减度’。当形状参数α趋近于零,则GGD越来越集中在零值左右;当形状参数α为1时,分布是符合Laplace分布;当形状参数α为2时,分布是符合正态分布;当形状参数α趋近于 ∞时,GGD的极限分布将符合uniform分布。下图为α=0.7,β=10,µ=0时,广义高斯分布的密度函数图,在零点时函数处于顶峰,当x趋于两端时函数逐步减小趋于0.
(图1)GGD分布密度函数图
2.2 参数α,β的矩估计
由于广义高斯分布是关于x=µ对称,不妨假设当µ=0时的情况,运用矩估计对其形状参数和均值参数估计,
(2.2.1)β的矩估计
首先求其二阶中心距;
 所以
所以 ,
,
则令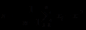 ,
,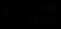 。
。
(2.2.2)α的矩估计: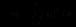
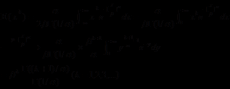
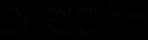
所以可以得到:
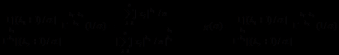
α的矩估计为 , (2.1)
, (2.1)
当 ,
, 取2和1时,
取2和1时,
 (2.2)
(2.2)
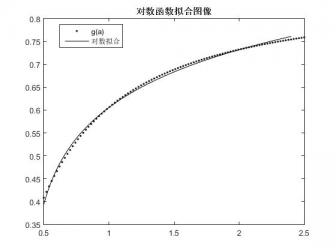
在文献[5]中介绍了一种简单方便的估计方法,大致为用似然比函数估计形状参数α和尺度参数β,通过指数函数和双曲线函数用最小二乘法去拟合估计函数g,得出估计函数g的拟合 ,然后求出拟合函数
,然后求出拟合函数 的反函数,用来近似估计函数g的反函数,则ɑ就可以通过(2.1)式得到。通过试验和计算比较分析得出双曲线拟合得到的结果有高精度和有效性更强的优点,且文献的快速估计方法较于KS估计和X2估计更加方便,结果更接近。
的反函数,用来近似估计函数g的反函数,则ɑ就可以通过(2.1)式得到。通过试验和计算比较分析得出双曲线拟合得到的结果有高精度和有效性更强的优点,且文献的快速估计方法较于KS估计和X2估计更加方便,结果更接近。
(2.2.3)关于 :
:
在此需要考虑是否存在 ,若通过判断其
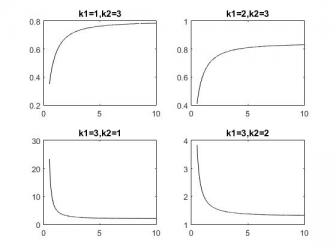
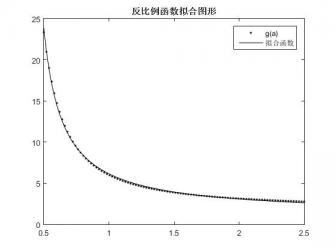
,若通过判断其 的正负,涉及的计算复杂,需要的篇幅很大。从另一方面考虑单调性,呈现g(α)图像,如下图(2)。可以看出在k1,k2,在不同情况下,都能很好的保持单调的性质。从而g(α)存在
的正负,涉及的计算复杂,需要的篇幅很大。从另一方面考虑单调性,呈现g(α)图像,如下图(2)。可以看出在k1,k2,在不同情况下,都能很好的保持单调的性质。从而g(α)存在 。
。
图(2)
(2.3)记α,β的似然估计:
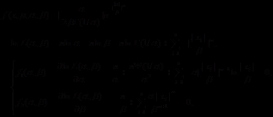

在α未知的情形时,由上述的方程组,要求出 的二元偏微分方程组,计算量庞大,因此上述途径取得估计参数复杂;若α已知的情行下,β的似然估计为:
的二元偏微分方程组,计算量庞大,因此上述途径取得估计参数复杂;若α已知的情行下,β的似然估计为:
 , (2.3)
, (2.3)
α可以运用上述矩估计的方法求得,再配合极大似然估计得到β,当观测样本足够大,且分布的形式已知时,最大似然(ML)估计是可靠性强的方法。
剩余内容已隐藏,请支付后下载全文,论文总字数:10733字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


