论文总字数：6898字

目 录

0、引言 5

1、问题的提出 5

2、一致收敛的定义 5

3、函数项级数非一致收敛的性质 5

3.1 连续性 6

3.2 可积性及逐项积分 7

3.3 可微性及逐项微分 8

4、函数项级数非一致性收敛的判定方法 9

4.1 利用端点发散性判别 9

4.2利用余项上确界的极限判别 10

4.3利用部分和函数的发散性判别 11

4.4利用和函数的连续性判别 13

4.5其他方法 14

5、结论 16

6、 讨论 16

参考文献 16

致谢 18

函数项级数的非一致性收敛

康伟振

，China

Abstract：The article analyzes the continuity, differentiability, integrability, and other properties of non-convergent function term series in which each term is continuous. Next we discuss several ways to determine the method the convergence whether the function item progression is convergent, such as the endpoint divergence, the limit of the exact bound on the remainder, and the divergence of the function. Some examples.

Key words：Function item progression; Uniform convergence; Non-uniform convergence；criterion

0、引言

判别函数项级数一致收敛的问题是数学分析课程中重要的知识点，在众多教材和参考书中给出了不少关于一致收敛的性质及其判别法.但对于非一致收敛的性质及其判别方法的研究较少.因此在本文中我们寻求函数项级数非一致性收敛所拥有的性质，同时利用其相关性质归纳出总结出函数项级数非一致性收敛的判别方法.在文献[1]中给出了函数项级数非一致性收敛与连续、逐项积分、逐项微分的关系.在文献[3]中给出了函数项级数非一致性收敛的几种判别方法,其中并没有仔细分类.在文献[4]中给出了函数项级数非一致性收敛三种判别方法，利用柯西准则、余项上确界，和函数连续性进行判定.其他文献中也给出了众多方法.我们将会在此汇总上述所有方法以及补充几种不常见的方法.

1、问题的提出

关于函数项级数一致收敛的问题是数分重要的知识点，但我们对于非一致收敛的性质的研究较少，平时在解决此类问题也感到十分困惑.因此在本文中我们寻求函数项级数非一致性收敛所拥有的性质，同时对参看文献中判别方法进行整理概括.

一致收敛的定义

定义1 设函数列与函数在同一数集上定义，，，使得时，，都有

，

则称函数列在上一致收敛于，记作

，.

定义2 若是函数项级数的和函数列，如果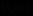在数集上一致收敛于和函数列，则称在上一致收敛于.

3、函数项级数非一致收敛的性质

我们知道函数项级数如果一致收敛，则其和函数将与拥有相同的性质，也就是连续、可导、可积，并且和函数积分和导数可逐步求积、逐步求导得到.原因是其求和、求积、求导运算顺序可以交换.

如果我们把一致收敛的前提去掉，我们将得出什么样的结论，其求和、求积、求导运算顺序是否还可以交换，一致收敛还是其必要条件吗?

3.1 连续性

定理1 如果函数项级数在上一致收敛并且连续，那么其和函数在上连续.

即

若函数项级数只是非一致收敛，那我们还能得到和函数连续的结论吗?接下来我们将举例说明，从而得出一致收敛与和函数连续之间的确切关系.

例1、函数项级数的各项连续，且在上有和函数

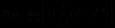
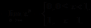
明显在区间上不连续

故级数非一致性收敛.

在此例中,函数项级数虽然连续，但其和函数并不连续.

例2、函数项级数在上有连续的和函数

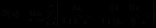
取

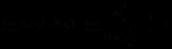
故级数非一致性收敛.

在上述例子中我们可得出一个结论：一致收敛仅是函数项级数连续的充分条件.

3.2 可积性及逐项积分

定理2 若函数项级数在区间上一致收敛，连续，则

剩余内容已隐藏，请支付后下载全文，论文总字数：6898字