论文总字数:9008字
目 录
1.引言 5
2.矩阵的初等变换及其性质 5
2.1矩阵初等变换的定义 5
2.2矩阵初等变换的性质 5
3.矩阵初等变换的应用 6
3.1行列式的计算 6
3.2将矩阵化简成行阶梯型和行最简型 6
3.3求矩阵的秩 7
3.4求可逆矩阵的逆矩阵 7
3.5求线性方程组的解 8
3.6判断向量组的线性相关性 10
3.7观察一向量可否由另一向量线性表达 11
3.8解向量组的秩和极大无关组 11
3.9判断两向量组是否等价 12
3.10将二次型化为标准型 12
3.11两个多项式阵最大公因子的求解 13
4.小结 17
5.参考文献 17
致谢 19
矩阵初等变换的应用
徐洋
, China
Abstract : The elementary transformation of matrices has a very wide range of applications in the processing of linear algebra problems. Through the elementary transformation of matrices transformed from the problem, some tedious and complex problems in higher algebra can be solved easily and clearly at a glance. This paper clearly points out the definition of matrix elementary transformation and some simple and easy-to-get properties. Through the understanding of the characteristics of elementary matrix transformation, it can be used flexibly in dealing with the corresponding types of linear algebra. In the study of advanced algebra, when dealing with a series of problems such as determinant values, solution of linear equations, linear space, linear transformation, quadratic type, etc., we can turn the problem into a corresponding matrix to solve. By using this method of transformation problems, we can simplify most of the problems in higher algebra, so the elementary transformation of matrices has an indelible role in the learning of linear algebra. In this paper, by enumerating the application of the elementary transformation of the matrix, expectation can help us to choose the appropriate method when dealing with various matrix problems, which can help us to improve the efficiency of the problem solving and master the details of the application of elementary matrix transformation and its specific operation.
Keywords: matrix; elementary transformation; property; application
1.引言
矩阵初等变换的起源,最早可以追溯到解线性方程组,人们在求解线性方程的过程中发现对方程组整行之间进行的一些变换,并不会改变线性方程组的值,由此引发了对矩阵初等变换的联想。由于在矩阵问题的处理中初等变换是解题的关键所在,因此在线性代数的学习中有着广泛的应用。在高等代数的学习中矩阵被作为重要研究对象,我们可以利用矩阵代替处理一些复杂的问题,其相关的应用可以在一般的高等代数和线性代数教材中找到 。初等变换法是高等代数中处理矩阵问题的最基本的方法之一,通过对矩阵初等变换及其应用的讨论可以加深我们对矩阵及其应用的理解,从而使我们可以更加灵活的利用矩阵的解决一些具体的问题。矩阵的初等变换通过对矩阵进行化简从而容易求矩阵的秩、求可逆矩阵的逆矩阵、判定向量组的线性相关性、求解线性方程组的解、化二次型为标准型等题目。此外,矩阵的初等变换也可以通过化简为求两个多项式的最大公因式、求特征值、求特征向量、求矩阵的若当标准型等一些问题提供了简单、实用的方法。矩阵的初等变换用在矩阵的行上或用在矩阵的列上所得到的作用是一样的。通过矩阵的初等变换把一个复杂的矩阵化简成一个相对简单的矩阵,由这个简单的矩阵我们可以得到原复杂矩阵的性质,是我们使用矩阵的初等变换解决复杂问题的一种最常用的方法。在解题的过程中我们可以发现在利用矩阵的初等变换求解可逆矩阵的逆矩阵时要比利用定义来做更简单准确,在化二次型为标准型时,将矩阵变换成对角阵的同时就能够得到相应的非奇异阵,容易理解和掌握,在用初等变换的方式求解矩阵特征值的时候相对来说容易方便,将求特征值的题目变为计算数的四则运算,通过使用矩阵的初等变换化解困难的问题解决了求矩阵特征值时求高次方程的根的难题,在求高阶矩阵的特征值时更能体现出使用这种方式的简便性。所以我们想要学好线性代数,首先必须熟练的掌握矩阵的初等变换。
。初等变换法是高等代数中处理矩阵问题的最基本的方法之一,通过对矩阵初等变换及其应用的讨论可以加深我们对矩阵及其应用的理解,从而使我们可以更加灵活的利用矩阵的解决一些具体的问题。矩阵的初等变换通过对矩阵进行化简从而容易求矩阵的秩、求可逆矩阵的逆矩阵、判定向量组的线性相关性、求解线性方程组的解、化二次型为标准型等题目。此外,矩阵的初等变换也可以通过化简为求两个多项式的最大公因式、求特征值、求特征向量、求矩阵的若当标准型等一些问题提供了简单、实用的方法。矩阵的初等变换用在矩阵的行上或用在矩阵的列上所得到的作用是一样的。通过矩阵的初等变换把一个复杂的矩阵化简成一个相对简单的矩阵,由这个简单的矩阵我们可以得到原复杂矩阵的性质,是我们使用矩阵的初等变换解决复杂问题的一种最常用的方法。在解题的过程中我们可以发现在利用矩阵的初等变换求解可逆矩阵的逆矩阵时要比利用定义来做更简单准确,在化二次型为标准型时,将矩阵变换成对角阵的同时就能够得到相应的非奇异阵,容易理解和掌握,在用初等变换的方式求解矩阵特征值的时候相对来说容易方便,将求特征值的题目变为计算数的四则运算,通过使用矩阵的初等变换化解困难的问题解决了求矩阵特征值时求高次方程的根的难题,在求高阶矩阵的特征值时更能体现出使用这种方式的简便性。所以我们想要学好线性代数,首先必须熟练的掌握矩阵的初等变换。
2.矩阵的初等变换及其性质
2.1矩阵初等变换的定义
下面的三种矩阵的变换类型被我们叫做矩阵的初等变换:
(1)两行之间相互调换(调换 两行,可以写成
两行,可以写成 );
);
(2)以数 和某一行的所有元素相乘(第
和某一行的所有元素相乘(第 行和
行和 相乘,可以写成
相乘,可以写成 );
);
(3)任意一行的 倍与另一行相对应的元素相加(第
倍与另一行相对应的元素相加(第 行的
行的 倍与第
倍与第 行相加,可以写成
行相加,可以写成 )。
)。
2.2矩阵初等变换的性质
(1)矩阵的初等变换不改变矩阵的秩;
(2)矩阵的初等变换对矩阵可逆与否没有变动;
(3)矩阵的初等变换对向量组的线性相关性没有改变;
(4)其中第一种初等变换可以由其它两种初等变换经过推导获得;
(5)设 是任意数域
是任意数域 上一个
上一个 矩阵,其中
矩阵,其中
 且
且 。若矩阵
。若矩阵 经过初等行变换变为矩阵
经过初等行变换变为矩阵

 ,其中
,其中 ,则
,则
 ;
;
- 对于
 的矩阵
的矩阵 进行一次初等行变换就相当于在其矩阵的左侧乘以对应的
进行一次初等行变换就相当于在其矩阵的左侧乘以对应的 初等矩阵,对
初等矩阵,对 做一初等列变换就相当于在其矩阵的右侧乘以对应的
做一初等列变换就相当于在其矩阵的右侧乘以对应的 的初等矩阵
的初等矩阵 ;
; - 如果
 级矩阵
级矩阵 为可逆矩阵,那么它可以分解成一些初等矩阵相乘的形式:
为可逆矩阵,那么它可以分解成一些初等矩阵相乘的形式:
 。
。
3.矩阵初等变换的应用
3.1行列式的计算
一般解法:经过初等行变换化为上三角形,如:
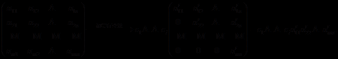 将行列式首行非零元下边的元都化成零,对角线上元相乘所得的数就是该行列式的解。
将行列式首行非零元下边的元都化成零,对角线上元相乘所得的数就是该行列式的解。
剩余内容已隐藏,请支付后下载全文,论文总字数:9008字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


