论文总字数:12601字
目 录
0、引言 3
1、问题的提出 3
2、预备知识 3
2.1定义概述 3
2.2定理概述 4
3、平面方程的形式与应用 5
3.1通过两个方位向量求点位式方程 5
3.2利用平面三点求三点式方程 6
3.3运用法向量求点法式方程 7
3.4使用待定系数法求一般式方程 9
4、典型例题分析 10
4.1利用平面束定理求平面方程 10
4.2二面角的角平分面方程问题 13
4.3求空间平面方程的一题多解 14
5、总结 21
6、讨论 22
参考文献 25
致谢 26
空间平面方程解法探讨
郭兴
,China
Abstract: Plane equation is the important topic in spatial analytic geometry, and solving space plane equations are common problems. First of all, this paper introduces different ideas of solving problems from the form classification of plane equations. Then, we solve problems by the tools of vector product and plane beam and compare different methods. Finally, this paper summarizes the skills of each solution, highlights the advantages and disadvantages of each methods, and extends this application.
Key words: Space plane; Plane beam; Equation
窗体顶端
窗体顶端
0、引言
在解析几何中,空间平面方程是最重要的内容之一.空间平面方程的形式种类繁多,例如点位式方程、三点式方程、点法式方程等等,因此求空间平面方程的解题思路、方法与技巧也有所不同.当我们阅读完一些解析几何教材及习题集时,我们会发现对于同一个题目,如果从不同的角度分析,采取不同的解题思路,就会获得不同的方法.经过对比就可以找出最适合本题的解决方式.因此,本文归纳总结了解析几何中求平面方程的经典题型,通过具体例题列举出对应的解题思路和方法,同时相互对比,分析各种解法的优劣之处.
1、问题的提出
空间平面方程的解法是解析几何中的重要课题之一.对于空间平面方程的求解方法和解题技巧让人应接不暇,从而在求解平面方程问题时让人思路混乱.因此,关于空间平面方程的解法的文章也浩如烟海.本论文通过先列举出空间平面方程的常见形式,进而引出不同的解题思路,并在解题过程中熟悉每种方法,接着处理一些稍微复杂的例题,从易到难,这也符合人们的学习习惯.并且在解题过程中我们会发现有的所谓的难题就是基本题型的组合,若能一步一步分解开就能解决.同时有些例题也使用了一些带有技巧的解法,和原来的解法做出比较,我们就可以不仅能解题,还能快速准确解题.这样,既有助于提升我们对重要知识点的把握,也有助于往后的学习.
2、预备知识
阅读文献[1]至文献[3],先对求解平面方程问题的过程中所需的相关定义定理有初步的了解.然后在解题过程中,进一步地体验到其意义,并且熟练应用,进而可以寻求解决空间平面方程最简便的解法.
2.1定义概述
向量、平面束等是处理空间平面的重要工具,在求解平面方程中有着广泛的应用,我们只有熟知它们才能在解题过程中灵活使用.所以接下来我们就对所需要的重要定义进行简单的了解.
定义1[1] :两个向量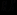 的模与它们的夹角余弦的乘积称为向量
的模与它们的夹角余弦的乘积称为向量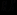 的数量积(内积),记作
的数量积(内积),记作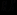 ,即
,即
 .
.
定义2[1] :两个向量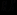 的向量积(外积)记作
的向量积(外积)记作 ,它们的模为
,它们的模为
 .
.
方向垂直于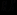 ,且
,且 构成右手标架.
构成右手标架.
定义3[1] :三个向量 的混合积记作
的混合积记作 ,其数值等于先作前两个向量
,其数值等于先作前两个向量 与
与 的向量积,再作所得的向量与第三个向量
的向量积,再作所得的向量与第三个向量 的数量积,即
的数量积,即 .
.
2.2定理概述
通过2.1的定义复述,我们初步认识了向量的计算定义.但在求解平面方程问题时,仅了解这些定义是不够的.因此,接下来我们要进一步探讨它们在解题过程中需要的定理应用.
定理1[1](数量积公式) :在右手直角坐标系 下,用向量的分量来表示数量积,
下,用向量的分量来表示数量积,
设 ,那么我们有
,那么我们有
 .
.
定理2[1](向量积公式):在右手直角坐标系 下,用向量的分量来表示向量积,
下,用向量的分量来表示向量积,
设 ,那么有
,那么有
 ,
,
或写成
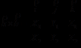 .
.
定理3[1](混合积公式):在右手直角坐标系 下,用向量的分量来表示混合积,
下,用向量的分量来表示混合积,
设 ,那么有
,那么有
 .
.
注:混合积为零的几何意义是 三向量共面.
三向量共面.
定理4[2](曲面的切平面方程):设曲面方程为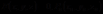 是曲面上一点.假设函数
是曲面上一点.假设函数 在
在 处可微且各偏导数不同时为零,那么
处可微且各偏导数不同时为零,那么 处切平面方程为
处切平面方程为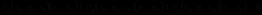 .
.
定理5[1] (空间平面束原理):如果两个平面

交于一条直线 ,那么过
,那么过 的所有平面可以写成
的所有平面可以写成
 ,
,
其中 是不全为零的任意实数.在平面不过
是不全为零的任意实数.在平面不过 的条件下,平面方程可简化为
的条件下,平面方程可简化为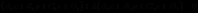 .当
.当 时,平面的极限为
时,平面的极限为 .
.
定理6[1] (点到平面距离公式)点 到平面
到平面 的距离为
的距离为 .
.
3、平面方程的形式与应用
在第2节中我们对解决平面方程问题所需要的定理进行了系统回顾.这一节我们对空间平面方程的常见形式做个归纳,从而引出求解空间平面方程的方法.这样在我们遇到具体的问题时便于有的放矢.
3.1通过两个方位向量求点位式方程
剩余内容已隐藏,请支付后下载全文,论文总字数:12601字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


