论文总字数:10377字
目 录
摘要 1
Abstract 2
1前言 3
2系统的基本概念及稳定性定义 4
2.1系统的定义 4
2.2系统稳定性的相关概念 5
3李雅普诺夫稳定性理论 7
3.1李雅普诺夫方法 7
3.2李雅普诺夫方法的应用和推广 10
4李雅普诺夫方法在无限维系统中的应用 15
4.1无限维系统的概念 15
4.2无限维系统最优控制的逼近 16
5总结 20
参考文献 20
致谢 21
李雅普诺夫方法在系统控制中的应用
谢宝群
,China
Abstract:In this paper, we first introduce the description of the system’s state space and the definition of stability of the system. Secondly, we introduce the application of the Lyapunov method and the extended Krasovsky method. Finally, we introduce the concept of optimal control on an infinite-dimensional system and approximate to the optimal solution by iterating the solutions of operator Lyapunov equations.
Key words:Stability of the system; Lyapunov method; infinite-dimensional system; optimal solution
1前言
俄国数学家李雅普诺夫于十九世纪末发表了论文[1],文中依据数学分析中的极限论思想,用 语言精确定义了系统稳定性的概念,还总结出了两种判别系统稳定性的方法:其一是通过求解状态方程,然后依据系数矩阵特征值的正负关系判别,其二则是构造特殊函数,然后依据构造的函数及其导数的正负定关系判别。
语言精确定义了系统稳定性的概念,还总结出了两种判别系统稳定性的方法:其一是通过求解状态方程,然后依据系数矩阵特征值的正负关系判别,其二则是构造特殊函数,然后依据构造的函数及其导数的正负定关系判别。
系统的稳定性最早可以采用诸如奈奎斯特判据和劳斯判据等方法进行判别。佟婷婷在[2]中总结了一些判别线性系统的稳定性判据。例如劳斯判据,其判别步骤如下:首先对系统的输入输出方程进行拉普拉斯变换,然后将二者相比得到系统的传递函数,并列出传递函数的特征方程:

接着依据特征方程的系数列出劳斯表,最后由所求得的劳斯系数的正负关系,就能够判别出系统是否稳定。
因为李雅普诺夫第二方法可以不必解出系统的状态方程,就能得到相对准确的结果,从而在目前的生产科研当中使用广泛,但是就一般而言,人们并没有找到一种可以适应所有系统的李雅普诺夫函数的构造方法。任斌在[3]中针对某些种类的系统,归纳总结出了几种李雅普诺夫函数的可能形式。例如,当系统为二阶定常系统时,该函数可能构造的形式为:
 为正整数。
为正整数。
而对于诸如以下形式的非线性系统:
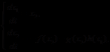
该函数可能表示为以下结构:

系统的最优控制,就是通过改变外界对系统的控制,使得系统的功能按特定指标达到最值的过程。李训经在[4]中指出:对于状态方程为 的系统,记满足初值条件的解为
的系统,记满足初值条件的解为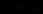 ,则最优控制就是使得功能指标
,则最优控制就是使得功能指标 达到最小值的
达到最小值的 。
。
当 ,
,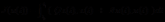 时,最优控制可以表示为:
时,最优控制可以表示为:

其中 使得以下Riccati方程成立:
使得以下Riccati方程成立:

本文在以上文献的基础上,首先引入了系统的状态空间描述以及稳定性的基本概念,然后介绍了李雅普诺夫第一,第二方法以及使用其判别系统是否稳定的相关定理,接着通过相关例子介绍在第二方法基础之上推广的克拉索夫斯基方法,最后在无限维系统中引入最优控制的概念,依据相关定理总结出可行算法,通过解算子李雅普诺夫方程所得到的一系列矩阵,不断迭代从而逼近最优解。
2系统的基本概念及稳定性定义
本节主要介绍系统的定义和状态空间描述,并在此基础上给出系统稳定性的定义,分类及其几何解释。
2.1系统的定义
系统是一些相互联结或制约的元件所组成的一个整体,可以用下图表示。

图1:系统的方框图表示
图中,方框代表系统,方框外象征系统的外部环境。 表示外部环境对系统的作用,称为系统输入;而系统在自身结构或者外界因素的影响下,做出对外部环境的作用,称为系统输出,用
表示外部环境对系统的作用,称为系统输入;而系统在自身结构或者外界因素的影响下,做出对外部环境的作用,称为系统输出,用 表示。以上二者共同组成了系统的外部变量。系统的内部变量指的是系统在不同时刻的运动状态,可以用
表示。以上二者共同组成了系统的外部变量。系统的内部变量指的是系统在不同时刻的运动状态,可以用 表示。系统的内、外部变量共同决定系统的运动情况。
表示。系统的内、外部变量共同决定系统的运动情况。
为了确保一个控制系统能够稳定地运行,我们首先要建立能够反映系统特点的数学模型,这个过程称为系统的状态空间描述。下面我们简单介绍一下相关的概念。
我们称能够完全地表征系统运动情况的一组向量为系统的状态向量,可用如下n个相互独立的变量 所组成的向量
所组成的向量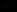 表示:
表示:
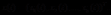 (2.1)
(2.1)
系统的状态空间,就是以变量 为坐标轴,所形成的n维空间,而空间中的任意一点表示某时刻系统的运动情况。对于表示系统状态变量和输入变量关系的微分方程,我们称其为系统的状态方程。一般可用如下非线性微分方程组表示:
为坐标轴,所形成的n维空间,而空间中的任意一点表示某时刻系统的运动情况。对于表示系统状态变量和输入变量关系的微分方程,我们称其为系统的状态方程。一般可用如下非线性微分方程组表示:
 (2.2)
(2.2)
而系统的输出方程,则是形容系统的外部变量和状态向量之间关系的数学表达式。一般可用如下方程组表示:
 (2.3)
(2.3)
系统的稳定性,就是系统遭遇外界扰动之后,依然能够维持平衡状态或者被控制在有界区域的动态属性。
2.2系统稳定性的相关概念
我们在研究系统稳定性问题的时候,一般只考虑没有特定输入作用的系统,称这类系统为自治系统,可用以下方程描述:

若上述微分方程满足解的存在唯一性条件,并且所求出的解在初始条件下是连续相关的,那么由状态空间中的某一点 所引起的运动可以表示为:
所引起的运动可以表示为:

我们称上述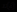 为系统的受扰运动,可用从
为系统的受扰运动,可用从 出发的一条曲线表示。
出发的一条曲线表示。
系统的平衡状态,就是状态空间中各个分量关于时间的导数为零的位置。就自治系统 而言,若对于任意
而言,若对于任意 均有:
均有:

那么 就是系统的平衡状态。
就是系统的平衡状态。
接下来我们介绍系统稳定性的定义。
在李雅普诺夫的意义下,一个稳定的系统指的是:仅仅凭借自身的结构特点,就能使得偏离平衡状态的受扰运动,依然能够回到平衡状态或者是平衡状态周边有限的区域内的系统。用数学的语言表示如下:
在区域: 内,对于
内,对于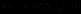 ,使得从
,使得从 内任意位置
内任意位置 出发的一切受扰运动都满足以下条件:
出发的一切受扰运动都满足以下条件:
 (2.4)
(2.4)
那么称平衡状态 稳定。当一个系统中所有的平衡状态都是稳定的,那么该系统稳定。
稳定。当一个系统中所有的平衡状态都是稳定的,那么该系统稳定。
剩余内容已隐藏,请支付后下载全文,论文总字数:10377字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


