反常积分及应用

论文总字数：10753字

目 录

1引言 ……………………………………………………………………1

2定义 ……………………………………………………………………1

2.1反常积分的定义 ……………………………………………………………………………1

2.2两种反常积分的定义 ………………………………………………………………………2

2.2.1无穷区间上的反常积分 ………………………………………………………………2

2.2.2无界函数的反常积分 …………………………………………………………………2

3敛散性 …………………………………………………………………2

3.1无穷积分的基本性质与收敛判别 …………………………………………………………2

3.1.1无穷积分的基本性质 …………………………………………………………………2

3.1.2非负无穷积分的收敛判别法 …………………………………………………………3

3.1.3一般无穷积分的收敛判别法 …………………………………………………………4

3.2瑕积分的基本性质与收敛判别 ……………………………………………………………5

3.3无穷积分收敛的必要条件 …………………………………………………………………5

3.4对数判别法 …………………………………………………………………………………9

4应用 ……………………………………………………………………14

4.1反常积分与无穷级数 ………………………………………………………………………14

4.2反常积分在概率统计中的应用 ……………………………………………………………14

4.2.1反常积分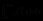…………………………………………………………………14

4.2.2反常积分…………………………………………………………………15

4.2.3反常积分…………………………………………………………………16

5结束语 …………………………………………………………………16

参考文献 ………………………………………………………………17

致谢 ……………………………………………………………………18

反常积分及应用

田凡

, China

Abstract:Improper integral is one of the very important part of the analysis research of mathematics. It can be mainly divided into improper integral with unbounded function and improper integral with unbounded interval, and they can be converted to each other. This paper firstly introduces improper integral from its properties, basic test of convergence and divergence and so on. In particular, we will introduce some necessary conditions of convergence, a necessary and sufficient condition, the logarithmic test and the new logarithmic test. Finally, we will introduce the relations between improper integral and series, and the applications of improper integral with unbounded function, especially, in Probability Theory and Mathematical Statistics. In this way, our students can understand the improper integral more thoroughly, realize the close contact between improper integral and our real life, and enhance the understanding of the value of practicality of mathematics.

Key Words: improper integral; central limit theorem; series; logarithmic test; convergence and divergence.

1. 引言

目前，随着社会的发展，汽车普及、高楼林立、工厂增多，噪音问题应运而生，如何解决噪音污染便成为了当代人关注的一个重点。此时，应用于通信理论、信号处理、图像处理的中心极限定理[1]开始被人们广泛关注，而中心极限定理，其实质上就是反常积分的应用。

反常积分在数学学科中的分析学方向，具有重要的地位，它是在定积分的基础上被提出，通过对定积分定义中两个必须符合的基本点的推翻，获得了两种常见的反常积分，即由区间无穷的所得——无穷积分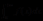，及由函数无界的所得——瑕积分。容易看出，两者可以相互转换：

为了进一步研究反常积分，首先，我们需要能够对一个反常积分是不是收敛有一个基本的判断。在数学分析中，我们已经学习了比较判别法、Cauchy判别法、Dirichlet判别法以及Abel判别法[2]，但是，对于一些形式特殊的函数，上述常规方法无法判别或是判别过程较为复杂，对此，人们提出了对数判别法[3],以及在进一步研究与改进下提出了新的对数判别法[4]。当可以判别一个反常积分收敛与否后，尤其是对收敛的反常积分，除了例如线性性质等一些基本性质外，本文将着重考虑它收敛的必要条件[5],即对于收敛的反常积分，当满足某些条件后，它会有一些比较好的性质以供使用。除此以外，我们还将探讨反常积分收敛的一个充分且必要条件，以便可以更加深入的了解反常积分。

数学与实际生活联系紧密，反常积分更是应用广泛，它贯穿于理学、工学、经济学等多个领域，本文将重点从理学中的数学方面介绍几种反常积分的运用[6]，尤其是它对于概率论与数理统计课程中方差、数学期望的证明，与中心极限定理以及密度函数相关的应用，将被我们用来进行具体的讨论。

1. 定义

2.1反常积分的定义

对于定积分，有两个不能违背的基本点：①有限的积分区间②有界的被积函数据此，对于反常积分，我们有两种形式的定义[7]：

定义2.1 如若①和②中至少有一个不符合，则称这类“积分”为反常积分。

定义2.2 如若将①中的有穷区间变成为无穷区间（或），或将②中上的有界函数更改为上的无界函数，则称这类“积分”为反常积分。

2.2两种反常积分的定义

2.2.1 无穷区间上的反常积分

定义2.3 设在无穷区间上是有定义的函数，对于所有有限区间是可积的，若极限存在，则称此极限为在上的无穷限反常积分，简称为无穷积分，记为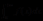，即，此时称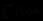收敛，否则，则称发散。

2.2.2 无界函数的反常积分

剩余内容已隐藏，请支付后下载全文，论文总字数：10753字