论文总字数:7259字
目 录
1、引言 4
2、柯西不等式的证明 5
2.1 引理 5
2.2 定理 5
2.3 柯西不等式的证明方法 5
2.4 定理 7
3、柯西不等式的应用 7
3.1柯西不等式在初等数学中的应用 7
3.2 柯西不等式在高等数学中的应用 9
4、柯西不等式的推广及应用 13
5、结论 15
6、讨论 16
参考文献 17
致谢 18
浅析柯西不等式及其应用
张羽波
,China
Abstract: Cauchy inequality is one of the most important and commonly used basic inequalities. It has different manifestations in different areas of mathematics, and there are many ways to prove it.Moreover, Cauchy inequality has both in elementary and higher mathematics. Extensive applicat-ions. The flexible use of Cauchy inequalities can simplify some complex problems and solve pro-blems in one step. This thesis focuses on Cauchy inequality, through the reading and summarizing of references. There are three kinds of common proof methods of Cauchy inequality, and through examples,The example shows that Cauchy inequality is widely used in extreme values, geometry, algebra, solving equations, etc. Finally, the generalization of Cauchy inequality is given. And it is application.
Key words: Cauchy inequality; Proof; Application
1、引言
我们知道,不等式的学习遍及数学的每一个分支,从小学到大学,不等式的学习贯穿到整个数学体系中.柯西不等式作为非常重要和经典的不等式,当然也在初等和高等数学中都起到了非常重要的作用.然而,在初等数学中,我们遇到关于不等式的题型时,对柯西不等式的结论是直接运用,包括在高等数学中也是,对柯西不等式的证明很少见到,对参考文献的阅读与总结,发现对柯西不等式的证明方法也很多.为此,本文选取了三种常见的证明方法:拉格朗日恒等式法[4]、构造辅助函数法[6]、构造向量法[7].此外,柯西不等式在不同的数学学科中它的表现形式不一样,本论文也给出了柯西不等式的三种推广形式及其应用,通过运用推广形式解题可以清楚的看到解题的简介性,也进一步说明柯西不等式的广泛运用.通过对文献[9]到文献[13],以及文献[15]和文献[17]的阅读,另外文献中也给出了很多例题,自己对例题进行改编,运用柯西不等式进行证明与求解,也得出了正确的答案.
柯西在研究数学问题中的“流数”问题时获得了十分著名的不等式叫柯西不等式的,柯西出生在巴黎, Cauchy-Buniakowsky-Schwarz不等式也叫做柯西不等式,它是柯西不等式的全称,是后两位数学家在原柯西不等式上面作进一步推广和改进,于是得到了现在加倍完善柯西不等式.而且,因为不等式应用的广泛性,故对柯西不等式的研究也引起了很多数学家的兴趣,而且也得到了许多著名的不等式,为此,不等式的发展得到了进一步的推广.匡继昌教授的《常用不等式》[1]收录了很大一部分著名的不等式,为不等式的研究提供了巨大的贡献,在1965年,Callebaut D K[2]推广了柯西不等式的形式为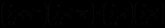 ,此外,柯西不等式的推广和应用可以促进人的发散思维,对一些题目也可以进行举一反三.
,此外,柯西不等式的推广和应用可以促进人的发散思维,对一些题目也可以进行举一反三.
2、柯西不等式的证明
2.1 引理
设 以及
以及 ,则有等式
,则有等式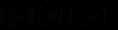
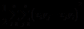 成立,该等式被称为拉格朗日恒等式.
成立,该等式被称为拉格朗日恒等式.
2.2 定理
设 以及
以及 ,我们可以有
,我们可以有
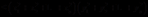 ,或者可以写成
,或者可以写成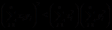 成立,此不等式为著名的柯西不等式,等号成立的充要条件是
成立,此不等式为著名的柯西不等式,等号成立的充要条件是 (常数)时.
(常数)时.
注[3]:对 都成立,我们称
都成立,我们称 为不等式的变量,且变量的数目是有限的,而此不等式表达了某些有限和之间的关系,则称这种不等式为初等不等式或有限不等式,而且,最基本的不等式都是有限的.
为不等式的变量,且变量的数目是有限的,而此不等式表达了某些有限和之间的关系,则称这种不等式为初等不等式或有限不等式,而且,最基本的不等式都是有限的.
2.3 柯西不等式的证明方法
柯西不等式的证明方法有很多种,本论文通过对参考文献的认真阅读与总结,选择了其中三种简单易懂的证明方法.
证法1 (拉格朗日恒等式法)由引理2.1可得
因为 
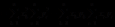
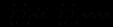



所以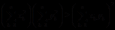 成立
成立
当且仅当 时,等号成立.
时,等号成立.
备注[5]:当k=2时
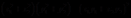


故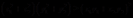 成立.
成立.
证法2 (构造辅助函数法)
设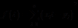
把 展开可得
展开可得


因为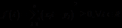
所以根据一元二次函数的性质得 .即:
.即:

则

故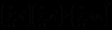 .
.
如果方程 至少有一个实根,等号成立,即
至少有一个实根,等号成立,即 (常数)
(常数)
证法3 (构造向量法)
2.4 定理
在欧式空间中,取两个向量  有
有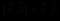 ,等号成立的条件是当
,等号成立的条件是当 线性相关[7].
线性相关[7].
设 ,
, 是两个
是两个 维向量,
维向量,
则 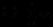 (1)
(1)
剩余内容已隐藏,请支付后下载全文,论文总字数:7259字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


