环的素理想、极小理想与极大理想

论文总字数：14443字

目 录

摘要 ……………………………………………………………………Ⅰ

Abstract…………………………………………………………………Ⅱ

1引言与预备知识 ………………………………………………………1

1.1环的概念 …………………………………………………………………………………1

1.2环的同态、理想 …………………………………………………………………………2

2 环的素理想 ……………………………………………………………3

2.1素理想的概念 ……………………………………………………………………………3

2.2特殊环的素理想 …………………………………………………………………………5

2.3素理想的存在性及性质 …………………………………………………………………7

2.4半素理想、素环及半素环 ………………………………………………………………8

3 环的极大理想与极小理想 ……………………………………………9

3.1极大理想的概念 …………………………………………………………………………9

3.2特殊环的极大理想 ………………………………………………………………………11

3.3极大理想的存在性及性质 ………………………………………………………………12

3.4局部环、含幺极大理想环 ………………………………………………………………13

3.5极小理想的概念及性质 …………………………………………………………………13

4 环的素理想与极大理想的关系 ………………………………………14

5 结果与讨论 ……………………………………………………………15

参考文献 …………………………………………………………………16

致谢 ………………………………………………………………………17

环的素理想、极小理想与极大理想

史叶萍

，China

Abstract：In this article,we mainly discuss the concepts of prime ideals, maximal ideals, and minimal ideals.And then we explore these ideals in some special rings , such as integer rings, residual rings, and domains. First, by understanding the definitions, we will have a basic grasp of these concepts,and then we can derive some equivalent decision theorems.What is more,by way of inferring and generalizing the theorems we have acquired,we can conclude what properties these ideals have and under what conditions these ideals exactly exist.Furthermore,we are going to find out the relationship between these ideals.On the one hand, we can use the definition, the theorems to determine whether the ideal is a prime ideal or a maximal ideal.On the other hand, we can also construct a special ring as a domain or a field by the prime ideals and maximal ideals we have known .

Key words：prime ideal;minimal ideal; maximal ideal;prime ring

1. 引言及预备知识

在代数学中，集合显然是我们最为熟悉，也是最先接触的一个概念。而在集合上可以进行一些延伸，例如可以定义n元运算，从而构成了各种代数系。当n=1时，群的概念应运而生；当n=2时，环就是其中最为常见的一类，当然，n也可以取其它任意整数，但群与环是最为基础的。

可以发现，环可以视为在群上添加新的定义和运算而形成，所以环的许多性质可以与群相联系。对于群而言，群有子群，相应的，环也有子环；子群中有性质较好的正规子群，从而我们定义出了商群，同样的，子环中性质较为良好的定义为理想，也是本文主要讨论的，商环的概念也从而加以定义。

理想作为具有吸附性的特殊子环，在环论中有着举足轻重的作用。理想可以决定环的同态（由环的同态定理），理想中最为常见的几种如下：主理想、素理想、极大理想与极小理想等。在下文中，我们将具体讨论上述理想的概念及相关性质。

首先，我们先介绍一些环与理想的一些基础概念。

• 1. 环的概念

定义1.1.1 设集合,定义加法运算与乘法运算，当下列条件成立时，称为环:

1. 构成交换群：
2. 构成半群:
3. 乘法关于加法具有左、右分配律：

我们通常把省略，用表示。

例1.1.1在整数集Z中，两种运算分别定义为加法和数乘，则显然满足构成环的条件，则Z是环。

同理，上面的集合Z可以换成其他的常见数集如Q、R、C，也能够构成环，一般将这些统称为数环。同样，我们也能构造许多类似的环，例如高斯整数环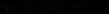：关于加法与乘法是个环；整数的剩余类环；等。

例1.1.2 设S是由全体n阶矩阵组成的集合，那么，将运算定义为矩阵的加法和乘法，则构成了矩阵环。矩阵的元素所在的集合也可以取任意常见的数集，构成的环叫作n阶方阵环。

定义1.1.2 在环中，满足：，那么，称0为零元；若有元素满足：，那么，称e是幺元或单位元，此时称R为幺环。

定义1.1.3设为一环，若满足交换律：，则称R为交换环。

例1.1.3 数环、多项式环为交换的幺环；由所有偶数组成的环2Z是交换环，但没有幺元；矩阵环不是交换环，但存在幺元。

定义1.1.4 在环中，，若H对于环R上定义的两种运算，即是一个环，那么就称H为R的，记作。

例1.1.4 ；。

定理1.1.1（子环的判定定理）设为环，，则有：

剩余内容已隐藏，请支付后下载全文，论文总字数：14443字