论文总字数:33701字
目 录
1 前言 4
1.1 研究意义 4
1.2 研究现状 4
1.3 研究内容 5
2 总二次电子能谱 6
2.1 俄歇电子谱 7
2.1.1 俄歇电子发射 7
2.1.2 俄歇电子谱的分类及应用 8
3 等离激元衰变激发二次电子的研究设想 8
3.1 等离激元的研究现状 8
3.2 研究方案的设想 9
4 二次电子发射的应用 9
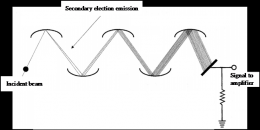
4.1 在电子倍增器上的应用 10
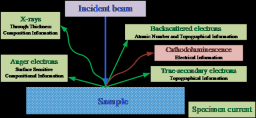
4.2 在表征技术上的应用 10
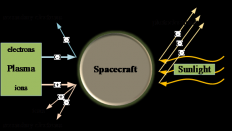
4.3 在航天器充电上的应用 11
5 二次电子能量分布公式的推导 12
5.1 二次电子发射的主要物理过程 12
5.1.1 内二次电子的激发 12
5.1.2 内二次电子的传播 13
5.1.3 内二次电子克服金属表面势垒并逸出 14
5.2 二次电子的能量分布 14
5.3 射程R和平均逸出深度的表达式 16
5.4 结果与讨论 16
6 结论 19
参考文献 20
致谢 24
附录 25
在学期间发表的论文 31
金属二次电子能谱的理论研究
木留华
, China
Abstract: In this paper, firstly, we introduced the properties of Auger Electron Spectrum and Plasmon, which relate to the total-secondary electron spectrum. We also introduced some significant applications of secondary electron spectrum. Secondly, on the basis of the three physical processes and characteristics of secondary electron emission and the energy band of metals, the formula for energy distribution of secondary electrons F(E,R) emitted from metals is deduced, where E and R are the energy of secondary electrons and range of primary electrons, respectively; E is measured from vacuum level. Based on the formula for F(E,R) and relationship among R, material density ρ, incident energy of primary electron Ep0 and inelastic mean escape depth, the formula for F(E,R) produced by higher energy primary electrons hitting on metals except higher-ρ metals or high energy primary electrons hitting on higher-ρ metals F(E) was deduced. The energy distribution of low energy (0 eVlt;Elt;10 eV) secondary electrons emitted from metals FL(E) calculated with the deduced F(E) and a few parameters are compared with other author’s calculated results. Work function and Fermi energy strongly influence FL(E). At low Ep0(Ep0lt;1keV), Ep0 strongly influences FL(E), in particular for high-ρ metals. Finally, it can be concluded that the deduced F(E) can be used to estimate FL(E).
Key words: energy distribution of secondary electrons; work function; Fermi energy; incident energy of primary electron; metal.
1 前言
1.1 研究意义
当具有一定能量的电子轰击物体表面时,会引起电子从被轰击的物体表面发射出来,这种现象称为二次电子发射[1-5,27,31],包括入射电子产生的真二次电子(能量小于50 eV)和直接从物体表面上弹射回来的背散射电子(能量大于50 eV)。自1902年Austin和Starke发现二次电子发射现象至今的110多年间[1],随着人们对电子技术应用的增加,二次电子在很多应用领域表现出积极或消极的影响:一方面,不少需要电子源的器件利用材料表面的二次电子发射能力产生电子[2]。在电子倍增器和光电倍增管中,利用二次电子发射的倍增作用,即使是非常微弱的电流,也可以放大到几百万倍,从而做出跨度极高的电子管[3];在直观储存管、电视摄像管、储存管等电子束管中,二次电子发射与靶面工作的物理过程相关密切[4],该类器件的材料往往需要具备较高的二次电子发射系数。另一方面,二次电子发射现象会降低很多真空电子器件的性能,甚至因为二次电子发射产生的热效应使器件烧毁,如大功率和高功率微波器件、真空传输线等[2]。另外,在俄歇电子能谱仪、离子显微镜、扫描电子显微镜[5]和其他表面分析仪器里[6],不同类型的二次电子发射现象被广泛应用;在接触管、开关管和磁控管等管子里,二次电子发射现象也得到应用[7]。特别地,二次电子的发射能够严重影响航天器在太阳风下的稳定性以及其充放电过程,也能很大程度上决定聚变装置、自由电子激光、粒子加速器等大科学装置的性能,比如在加速器中,研究表明,加速器中产生电子云的主要原因之一是真空室的材料往往具有较高的二次电子发射系数,从而使得加速器在运行时,电子在真空室内发生严重的增值现象,导致电子云的形成。抑制电子云的主要措施之一就是抑制二次电子发射或者减小真空室材料的二次电子发射系数[8-10]。
可见,对二次电子发射的物理机理进行理论研究,对于人们在其广泛的应用中增强积极的影响、抑制消极的影响具有重要的实用价值。
1.2 研究现状
二次电子发射一直作为重要的研究领域被广大科技工作者关注,国内外对二次电子进行了广泛的研究[11-23],主要集中在二次电子能谱和二次电子发射系数的研究,主要研究方法是Monte Carlo模拟、物理理论研究和实验研究,以下重点论述主要的研究进展。
在Monte Carlo模拟方面,Schou(1979)总结发展了前人的理论成果[11]、Furman(2002)提出统计概率模型[12],均成功地通过Monte Carlo模拟计算,得到二次电子能谱和发射系数。我国的Ding Z J,用光电介质方程描述原电子能量损失和相关的二次电子发射过程,进而通过Monte Carlo模拟计算得到二次电子发射系数(2000),并对二次电子发射机理做出进一步评述[13];进一步地,Ding Z J通过应用Mott截面法描述电子的弹性散射过程[14],结合Monte Carlo模拟计算得到二次电子能谱(2008)。
剩余内容已隐藏,请支付后下载全文,论文总字数:33701字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;