论文总字数:13519字
目 录
1.引言…………………………………………………………………1
1.1 研究背景及意义………………………………………………………………………1
1.2 国内外研究现状………………………………………………………………………1
1.3 本文主要研究工作……………………………………………………………………2
2.二维电子气朗道能级半满时的热容…………………………………2
2.1 化学势的温度依赖性…………………………………………………………………3
2.2 半满时的热容…………………………………………………………………………4
2.3 通常情况概论…………………………………………………………………………7
3.二维金属电子气的量子态数…………………………………8
3.1 一维自由粒子………………………………………………………………8
3.2 二维金属电子…………………………………………………………………8
- 二维金属电子气的热力学量解析计算……………………………10
4.1 二维金属电子气的化学势……………………………………………………………10
4.2 二维金属电子气的内能……………………………………………………………14
4.2 二维金属电子气的热容……………………………………………………………16
5.结论…………………………………………………………………18参考文献 ………………………………………………………………18
致谢 ……………………………………………………………………19
二维金属电子气的热力学性质研究
罗振楠
物理与光电工程学院, 210026
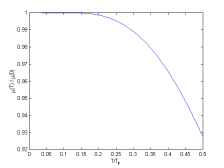
摘要:二维电子气(Two-dimensional electron gas,2DEG)是指电子气可以在二维方向自由移动,而在第三维上受到限制的现象。二维金属中的电子气为强简并的费米气体,遵循费米统计。本文通过理论计算,得到了在室温附近二维电子气的化学势、内能和热容的严格解析解,尤其通过数值计算二维电子气在室温附近的热容。计算结果表明,在温度高达0.01TF附近,电子气对热容的贡献为0.033R,仅为晶格振动热容的1.65%。
关键词:二维金属电子气,量子态数,化学势,热容
Thermodynamic properties of two dimensional metal electron gas
Luo Zhennan
School of Physics and Optoelectronic Engineering,NUIST, Nanjing 210026, China
Abstract: Two-dimensional electron gas(2DEG)refers to the electron gas can move freely on two-dimensional direction ,and in the third dimension is restricted.Electron gas in two dimensional metal is strongly degenerate Fermi gas,follow Fermi statistics.In this paper, the theoretical calculation,Strict analytical at room temperature near the two-dimensional electron gas chemical potential, internal energy and heat capacity of the solution is obtained.Heat capacity especially through numerical calculation of two-dimensional electron gas in the vicinity of room temperature.The calculation results show that, in a high temperature near the contribution of electron gas of heat capacity is 0.033R,Only the 1.65% lattice vibrational heat capacity.
Keywords: Two dimensional metal electron gas,Quantum state number,chemical potential,specific heat
1.引言
1.1 研究背景及意义
对金属自由电子气体的物理学性质研究一直以来都是物理学的兴趣和重点,如金属电子的磁振荡效应[[1]][[2]][[3]],二维电子气的霍尔效应,二维电子气的霍尔效应分为整数霍尔效应,分数霍尔效应,和非常热门的拓扑结缘体和反常霍尔效应都是对电子气的研究,如此可见对二维金属自由电子气的研究对于物理学界来说是非常重要的。在19世纪中的研究中,随着尤利乌斯罗伯特麦耶(Julius Robert Mayer)和赫尔姆霍茨赫尔曼(Hermann von Helmholtz )等人对有关于功和热的能量守恒定律的提出[[4]],随着热力学的理论初步形成,利用这些理论物理学家们用来研究嫡,温度,反应物态变化规律,宏观热力学的性质和现象等。在这期间,鉴于对原子结构的研究和微观动力学理论的发展而形成的统计物理理论,可以用来研究因大量粒子相互作用而引起的宏观物理特性,如:压强,内能,化学势等。随后,在玻尔兹曼一普朗克公式,克劳修斯嫡增原理S=KbLnW,及玻尔兹曼,吉布斯等提出的普遍性假设等一系列理论的基础上,逐步形成统计热力学理论。这样我们就可以研究在经典统计力学中没法确定的微观体系的微观态的各种性质[[5]]。
此后,随着普朗克的量子理论出现,人们对经典的统计热力学有了重新认识。物理学家利用波动力学中的随机性原理来解释经典统计物理学中对多粒子体系的的统计方面问题,如Landau及后来的von Neumann,Dirac相继提出的密度矩阵理论[[6]]。这样人们就可以研究一系列新的实验现象,如:Landau抗磁性,传导率量子化特性,量子霍尔效应,量子点等。
在量子力学及热力学统计物理理论的基础上,人们对能精确求解的物理模型进行了大量的研究和推导。例如:1907年,爱因斯坦的研究能说明在零温时比热趋于零的量子效应;Landau解决的关于电子在磁场中运动的量子力学问题;Peierls阐述的自由电子在磁场中的抗磁性的概念;Darwin解释了边界对抗磁性的作用,Fock对具有恒定磁场和抛物势阱的复合磁场中的运动(现在我们称作Landau-Fock-Darwin (LFD)模型)的研究;以及人们对LFD模型在谐振子势中的Landau抗磁性的研究[[7]]。
1.2国内外研究现状
低维物理问题一直是凝聚态研究的热点问题,因为在低维物理中有许多特殊性质,例如:一维金属环,在非超导的情况下具有持续电流;二维电子气因为有分立的朗道能级,出现了整数霍尔效应和分数霍尔效应等。这些复杂而重要的独特的量子物理特性是基于简单的Landau能级,所以Landau能级的讨论是很重要的。统计物理学中,尤其是费米统计中,解析解非常重要,它是计算和研究所有热力学函数的基础,因此有必要得到无相互作用作用的自由二维电子气的化学势和内能,进而讨论其物理性质。
Lifshitz和Kosevich对金属中电子气的dHvA效应中量子振荡展开的现象研究中作出了杰出贡献[[8]],由于dHvA效应被用于测量金属费米面,因此这项工作变得尤其重要。多年来对二维金属电子气体的dHvA效应研究层出不穷,得到了很多值得研究的结果。二维的dHvA效应最初由Peierls得出,他指出在零温时(T=0)理想二维电子气的磁化强度M随磁场的变化是呈锯齿形状的,1980年之后由于二维导体实验发展推动了对二维dHvA效应很多新理论的研究[[9]],例如,Vagner和与他的合作者的一些工作,他们得到了化学式和磁化强度随磁场强度变化的解析表达式,虽然这一工作中没有讨论材料参杂和朗道能级的能级展宽,但对于更复杂的情况有非常有益的借鉴作用[[10]]。Zawadski和与他合作者的工作,运用数值的方法研究了二维电子气的磁化强度等热力学量。 Shoenberg研究了在有限温度情况下二维电子气的物理性质,得到了一些近似的结果。Wang和O’ Connell研究了在强磁场近似下非零温度的二维电子气磁化强度的性质,在低温情况下他也得到了一个新的系统自由能的解析表达式。Champel和Mineev研究了一个分析dHvA效应的理论,对于满足条件 (
( 是系统化学式,
是系统化学式, 是点在磁场中运动时的旋转频率)[[11]],这理论对二维和准二维电子气在常规态和超导态的混合态下非常有用。
是点在磁场中运动时的旋转频率)[[11]],这理论对二维和准二维电子气在常规态和超导态的混合态下非常有用。
1.3本文主要研究工作
本文首先介绍狄拉克δ函数频谱和以及基于高斯函数的频谱两种态密度导出二维电子气的比热容,然后计算出二维金属电子的量子态数,最后根据量子态数计算出了二维金属电子气的化学势、内能和热容等热力学函数。
2.二维电子气朗道能级半满时的热容
由于二维层电子展示的行为并非典型性,并且易于在半导异质结构中实现,因此它们仍旧是物理学中的一个令人感兴趣的点。当前,对于二维电子气(2DEG)的研究旨在理解量子霍尔电导率和德哈斯-范阿芬尔效应或者所磁化振荡中的停滞时期。停滞时期中的平稳下降和振荡极值揭露出了扩展后的能级,也就是特征值En之间的有限态密度(DOS)。这些特征值En被称为朗道能级,是通过将一个强磁场(B)垂直或以相对倾斜的方向应用于系统“平面后得到的量子能谱(E)。En扩展的显著行为会产生其他奇异特征,这归因于系统出现的杂质、瑕疵和其他不均匀性所知道的失调。理想上,一个不互相影响的二维电子气的态密度在垂直强磁场中作为一系列的脉冲函数,也就是
(1)

其中的e是电子电荷,h是普朗克常数,是第n个朗道能级。在给定有效质量的回旋加速频率下,后者取决于强磁场。这种态密度结构能够用于模拟能量载体分布范围非常窄的真实物质。



通常,一个二维电子气态密度的真实形状取决于和实验测量的热容数据的理论契合。比如说,这个过程在GaAs-GaAlAs多分子层中的二维电子气中进行,能够在单一背景中产生带有高斯峰的态密度。因此,许多关于二维电子气系统热力学和磁特性的实验和理论研究都使用一种基于高斯函数的态密度形式,例如
(2)

这个等式通过参数将扩展也考虑在内。

在利用这个态密度的研究中,预测强磁场中的热容和其他磁热效应成为的通用函数,其中是Boltzmann常数,T为温度。但在电子浓度恒定时,它们的数值模拟无法提供与相关的这些热力学性质依存性。



周期矩形几何学中的另外一个无杂质量子霍尔系统研究发现,定容情况下的比热表现为,其中是基态和首次激发态之间的能隙。文献[[12]]中的数值模拟为填充系数v的不同值推导。填充朗道能级的这个名义数量表示为,其中N是电子浓度。对于各种不同的填充系数,它们上的结果产生的在温度低时有一个尖锐峰,高度取决于。然而它们的运算表明有限尺寸效应在温度低时占优势。由于没有精确的表达式,因此想要将行为与主要的晶格贡献在温度非常低的情况下区分开,那么就会很困难。一般来说,由于强烈地依赖于给定系统的性质,比如说态密度,作为电子结构产生的结构,想要的确切行为并不容易。













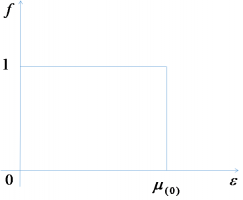
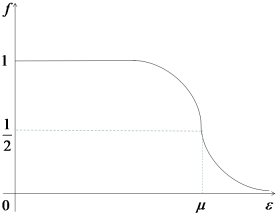
当化学势不随温度T而变化时,可以得到二维电子气系统的闭合解表达式。当最后一个占用的朗道能级半填充时,也就是最后一个占用的能级简并性填充至半满,后者在有限非零温度T下得到满足。不像带有单数分母的其他分数v,霍尔电阻中并没有观察到停滞时期,因此我们特别关注了v=1/2以及其他半填充状态。在半填充情况下,化学势证号位于朗道能级正中间,也就是扩展态所处的位置。这个v缺少一个间隙,有些实验还观察到了费米液体状态的特点。


针对带有三角形状或高斯态密度的不带自旋的二维电子气在磁场垂直应用时的情况,本文将详尽地推导(其中是一个奇整数)时的。首次获取了热容的确切关系,将其作为基础来表示电子气的基础态密度。此外,本文还为两个案例都设置了热容达到最大值时的条件,两者都包括它依赖的真实性质。对那些用于抵制温度变化的装置设计来说,这个特别有用。最后文章也会概述其他填充系数时的,从而系统阐述普遍情况。





2.1 化学势的温度依赖性
剩余内容已隐藏,请支付后下载全文,论文总字数:13519字
相关图片展示:
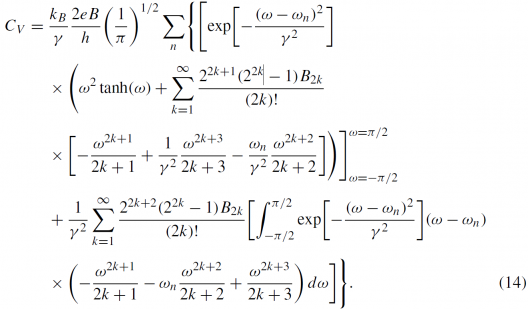
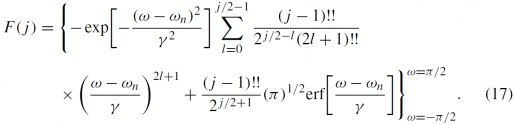
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


