论文总字数:13980字
目 录
一 引言···················································4
二 重离子碰撞········································4
(一)高阶矩·······························4
(二)QCD相变······························6
(三)碰撞试验······························8
三 重离子碰撞研究过程应用的统计概念············8
(一)中心极限定理····························9
(二)临界效应······························11
(三)QCD临界点·······························12
四 统计对相对重离子碰撞守恒量测量矩的影响·········12
(一)测量高阶矩的统计依赖性·······················12
(二)测量矩概率分布的统计相关性·····················13
五 结束语························16
参考文献·························18
致谢···························19
相对论重离子碰撞中高阶矩的统计分布
闫岩
Abstract: The QCD critical point location is one of the important goals of the Brookhaven National Laboratory Energy Scanner. Due to the limitation of the scale and the evolution time of the heavy ion collision system, the correlation length is too late in the vicinity of the critical point, and the traditional critical divergence effect can not be observed in the heavy ion collision. In the course of theoretical study we will find that the higher the order of conservation, the greater the ups and downs near the critical point. Therefore, the higher order moment has been widely used in the test to explore the QCD critical point. This article will discuss the impact of statistics on higher order moments. In the case of insufficient statistics, the distribution of higher order moments will no longer satisfy the central limit theorem. The higher the order of higher order moments, the greater the demand for statistics. For the fourth moment, the measurement is reliable only if the event is greater than one million.
Keywords: 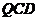 ; critical point; statistics
; critical point; statistics
一、引言
在自然界中有很多相互作用,其中最基本的只有四种,分别是:强,弱,电磁还有引力。在1930年前后,物理学家认为物质是由三种基本粒子构成:质子、中子还有电子。对我们来说,核是由质子和中子组成的,质子是正电荷的,如果你考虑电磁相互作用,质子和电子应该相互排斥的。 质子和中子在未充电时,是不带电的。 它如何与核结合的呢?事实上这是由强相互作用中的一些效应引起的。强相互作用大于电磁相互作用将近两个数量级。而这四种力的相对大小,我们可以假设引力相互作用为1,那么弱相互作用的大小为10的32次幂,电磁相互作用的大小为10的37次幂,强相互作用的大小为10的39次幂。
量子色动力学(Quantum Chromodynamics,简称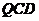 )是强相互作用的理论研究产物。量子色动力学成立于1973,至今不到半个世纪,但它对理论物理的研究做出了巨大的贡献。有研究表明,质子和中子是由更小的粒子:胶子和夸克。夸克有一个有色电荷,每个夸克有三种不同的颜色:红,蓝,绿。
)是强相互作用的理论研究产物。量子色动力学成立于1973,至今不到半个世纪,但它对理论物理的研究做出了巨大的贡献。有研究表明,质子和中子是由更小的粒子:胶子和夸克。夸克有一个有色电荷,每个夸克有三种不同的颜色:红,蓝,绿。
在低能量下,夸克是密切交织在一起的强子,运动不自由,这是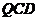 的一个功能---理论-夸克限制。但当能量足够高,夸克与胶子的强子内部会发生分离,达到自由的状态,即解除限制。
的一个功能---理论-夸克限制。但当能量足够高,夸克与胶子的强子内部会发生分离,达到自由的状态,即解除限制。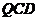 理论预言的夸克和胶子之间的耦合系数会逐渐减小到零,这时,动量会发生转移或能量会增加。这是
理论预言的夸克和胶子之间的耦合系数会逐渐减小到零,这时,动量会发生转移或能量会增加。这是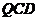 理论的另一个特征-进步自由。
理论的另一个特征-进步自由。
二、重离子碰撞
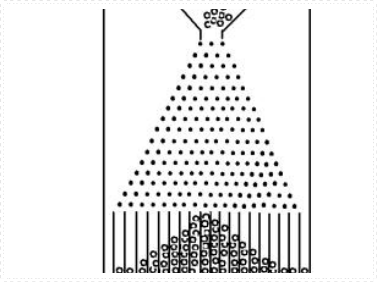
重离子碰撞的物理过程是核与核之间的强烈碰撞。入射能量的一部分被转换成核的内部激发能。当激发能上升一段时间后,他可以达到很高的程度,这个时候,核与核间的键就会断裂,核的整体也会碎裂,碎裂之后,就形成了许多不同的产物,这里所指的不同,是质量,这种过程我们就叫他多重碎裂。下图1-1是预言下的理论照片。
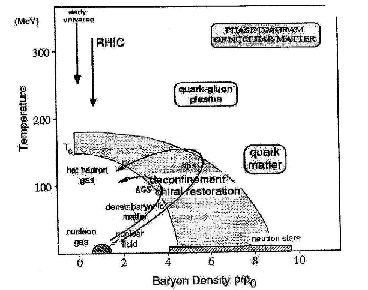
1-1 理论上的图片
2.1高阶矩的介绍
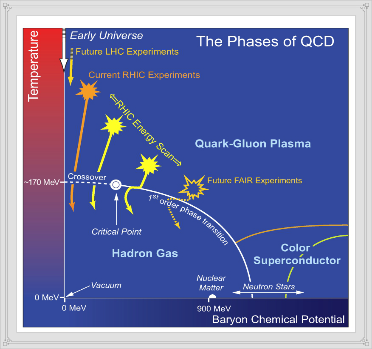
为了找到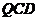 相变的临界点,我们很有必要知道临界点敏感的观测结果与约束的起伏和相变密切相关。在热平衡的情况下,通常我们会说波动的二次导数的分区功能,二次功能也就相当于数学二阶累积量,也就是感应率。现在,我们因该了解了,当位与临界点的时候,相关的长度会变得特别大,感应率也相应的会发散。但是,在相对论重离子碰撞试验中,因为有体系演变期间的限制,所谓相关长度的长度是有限的,而系统的尺度也是有限的。根据理论计算估计,相关长度
相变的临界点,我们很有必要知道临界点敏感的观测结果与约束的起伏和相变密切相关。在热平衡的情况下,通常我们会说波动的二次导数的分区功能,二次功能也就相当于数学二阶累积量,也就是感应率。现在,我们因该了解了,当位与临界点的时候,相关的长度会变得特别大,感应率也相应的会发散。但是,在相对论重离子碰撞试验中,因为有体系演变期间的限制,所谓相关长度的长度是有限的,而系统的尺度也是有限的。根据理论计算估计,相关长度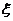 接近2.5调频,这是比系统的规模要小得多。在临界点时,它与此成正比,从而导致响应率不发散这种现象,所以我们需要更敏感的临界点来观察,近年来,起伏的高阶守恒电荷被认为是一个很好的研究方向,也是很好的临界点的检测方向。负载的高阶波动是高阶感应率或高阶累积量(统称为高阶矩)守恒的两个原因,第一,因为它们有更敏感的链路长度。例如,三阶矩与四阶矩成比例并且成正比。其次,需要告诫的是有一个非单一的步骤,因此,在临界点临近的地方有一个象征性的改变。如此一来,有可能在研究高阶矩的理论和讨论他们的关键行为的时候,就找到了一个临界点的实验。
接近2.5调频,这是比系统的规模要小得多。在临界点时,它与此成正比,从而导致响应率不发散这种现象,所以我们需要更敏感的临界点来观察,近年来,起伏的高阶守恒电荷被认为是一个很好的研究方向,也是很好的临界点的检测方向。负载的高阶波动是高阶感应率或高阶累积量(统称为高阶矩)守恒的两个原因,第一,因为它们有更敏感的链路长度。例如,三阶矩与四阶矩成比例并且成正比。其次,需要告诫的是有一个非单一的步骤,因此,在临界点临近的地方有一个象征性的改变。如此一来,有可能在研究高阶矩的理论和讨论他们的关键行为的时候,就找到了一个临界点的实验。
高阶电感的观测可以来自它的共轭变量的自由能。例如,磁化的电感可以来自自由能的磁化,除此,能量可以来自自由能的温度,观察这种反映的起伏。我们可以得到自由能与分配函数有下列关系,
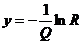
其中Q等于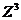 ,它表示立方晶格的体积,Z表示点阵的每个方向上的网格点的个数。并且,我们还可以得到各级磁感应率分别为:
,它表示立方晶格的体积,Z表示点阵的每个方向上的网格点的个数。并且,我们还可以得到各级磁感应率分别为:
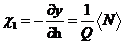 ,
,
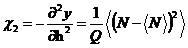 ,
,
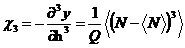 ,
,
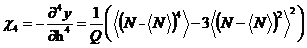 ,
,
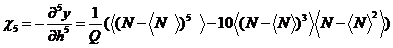 ,
,
在这里,X表示多次测量下不同自旋结构X的平均值。第一项是模型的参数量。去掉右边的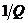 方程得到类矩的磁化(累积量),然后用
方程得到类矩的磁化(累积量),然后用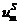 表示,这时候我们就能很清晰知道:
表示,这时候我们就能很清晰知道:
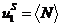 ,
,
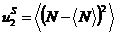 ,
,
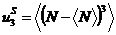 ,
,
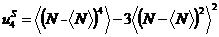 ,
,
剩余内容已隐藏,请支付后下载全文,论文总字数:13980字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


