论文总字数:15688字
目 录
摘要 1
Abstract. 2
第1章 绪论 3
1.1 肖特基势垒 3
1.1.1 肖特基势垒简介 3
1.1.2 肖特基势垒在半导体器件中的应用 3
1.2 隧穿现象及隧穿概率 3
1.3 隧穿概率之WKB方法简介 4
1.3.1 WKB方法 4
1.3.2 WKB近似法的基本思想 4
1.3.3 WKB近似法的基本步骤 4
1.4 遂穿概率之转移矩阵法简介 5
第2章 运用WKB近似以及矩阵转移法求隧穿概率 6
2.1 引言 6
2.2 WKB近似法求解简单三角形肖特基势垒隧穿概率公式 6
2.3 转移矩阵法求解隧穿概率 7
2.3.1 肖特基势垒情况下对薛定谔方程的处理 7
2.3.2 转移矩阵法计算隧穿概率 9
2.4 WKB近似法与矩阵转移法对比 10
第3章 肖特基势垒反向隧穿电流的计算模型与特征分析 12
3.1 引言 12
3.2 肖特基势垒反向隧穿电流的三种计算模型以及三者之间的关系 12
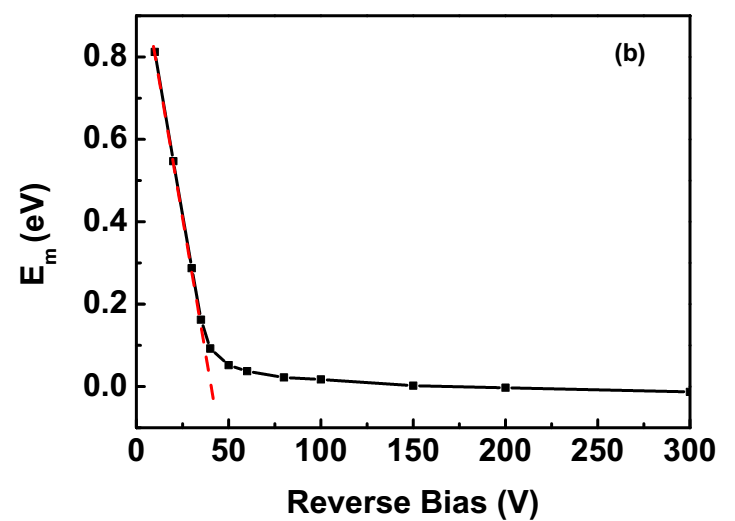
3.3 肖特基势垒反向隧穿电流特征 16
3.4 结论 21
参考文献 22
致谢 23
肖特基接触反向隧穿电流研究
曹栓子
,China
Abstract:This paper uses the WKB approximation method and the transfer matrix method is discussed under the uniform doping Schottky barrier tunneling probability formula, through the comparison of the two methods under the two formula, summarize the similarities and differences between the probability formula of WKB approximation method and the transfer matrix method, and the tunneling effect problem discussed these two methods the pros and cons. Calculation method to analyze the connection and difference between Schottky barrier reverse tunneling current field emission, thermal field emission and WKB integral approximate calculation model based on three models by numerical, elaborates on the problems of field emission and thermal field emission model. Numerical results by analyzing the integral calculation model of Schottky. The reverse barrier tunneling current is discussed with the basic characteristics of the energy distribution peak.
Key words:Schottky barrier tunneling probability; WKB approximation; matrix transfer method; thermal field emission; field emission; reverse leakage current
绪论
1.1 肖特基势垒
1.1.1 肖特基势垒简介
通常情况下半导体材料的电子逸出功是低于金属材料的电子逸出功的,在金属和半导体发生接触的情况下,半导体材料里可移动的电子在电子逸出功作用下通过两者的接触部分流入到了金属材料里,由于电子的流失,在半导体的外部就会逐渐出现由带有正电且不能移动的杂质离子形成的空间电荷区域且半导体材料的本身表现为正电性;而金属因为外部电子的流入表现为负电性,此时会产生电场,它的形成阻碍了半导体中电子的移动。在接触面处半导体能带产生了一些变化,进而出现了高势能区,称其为肖特基势垒区域。由于其整流特性等性质,肖特基势垒能够在一些方面得到应用。
1.1.2 肖特基势垒在半导体器件中的应用
因为肖特基势垒特有属性即它本身界面电压很低,肖特基势垒可以被当作理想二极管用于一些器件。一些电路的构思过程中,肖特基势垒也可以和普通的二极管以及其他的晶体管进行组合应用,之所以把它加入到电路中,是为了通过它的特性(界面电压较低)确保电路中余下的元件不受损害。但是在实验研究以及器件制造中,相比于那些人们所熟知的半导体器件,肖特基器件始终没有得到广泛的应用。下面例举一些将肖特基势垒应用于半导体器件的实例:比如肖特基二极管,高压肖特基二极管等等。而隧穿作为肖特基势垒一重要机理,在肖特基器件中起着关键的作用。
1.2 隧穿现象及隧穿概率
隧穿效应属于微观科学中一项重要研究,其包含于衰减波耦合效应这一领域。依据经典力学中相关知识,若是粒子所具有能量不高于势垒高度,那么粒子就不可能射入到势垒区域中,会悉数被势垒阻挡;仅在其所具有能量高于势垒高度情况下,粒子才会通过势垒的阻碍。然而,结合量子力学的相关知识进一步考虑,我们知道粒子是具有波动性的,那么隧穿就可以近似看作为波穿越具有体积的介质的情形,可知在粒子能量不低于势垒高度的情况下,粒子是有机会穿透势垒区域的;而在粒子能量不高于势垒的情况下,其也有一定机会穿透势垒区域。这类情况被研究者们称为粒子隧穿问题也被称为散射问题。量子隧穿效应属于量子特性中的一种,简单说来就是粒子进入并穿透以前无法越过的“墙”的状况。其根本在于微观粒子的波的性质,使得粒子有机会穿过“墙”。而隧穿概率则是指那些可以穿过势垒区域的粒子在总粒子数中所占据的比例。接下来我们将运用WKB近似和矩阵转法对具体情况下的隧穿概率进行求解。
1.3 隧穿概率之WKB方法简介
1.3.1 WKB方法
WKB近似法的全称叫做温侧-克喇末-布里渊近似法,其属于量子力学中的一种近似方法,同时也是半经典计算方法中的一个分支;时常被研究者用于解决一些量子力学中的问题。是以Gregor Went zel、Hendrit Anthony Kram ers和Leon Brillouin 三位物理学家的名字命名的。经过长期的研究,这三位科学家于1926年成功地将WKB近似法发展应用于量子力学的研究。又经过科学家们近百年的发展和改进,WKB近似得到了很好的完善和普及,得以被广泛应用:诸如用于处理量子力学中的谐振子问题、开普勒问题、一维定态微扰问题以及三维定态微扰问题等等。但由于WKB近似的使用中常常伴随着较大的计算量,所以运用起来有些复杂。
1.3.2 WKB近似法的基本思想
先对所研究问题中波函数进行对应幂级数展开,把其转换成指数函数的形式;然后再进行半经典展开,从而使得幂级数展开得到的结果近似于普朗克常量;再进一步将薛定谔方程转化为我们相对熟悉的常微分方程以及假设所研究问题中波函数的波幅或者相位的变动非常缓慢,最后通过详细推到和运算得出波函数的近似解,从而解决对应量子力学问题。
如果所研究的薛定谔方程可以被分解为几个常微分方程,而且研究的问题又与经典问题大致相同时,则可以将波函数按照幂级数的形式展开,只需要取前面少数的几项就能得到想要的结果。所谓的问题与经典问题大致相同,是指在所研究的体系中,研究的动量以及体系中运动的空间尺度较大,同时其中普朗克常量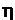 的作用并不突出。
的作用并不突出。
1.3.3 WKB近似法的基本步骤
对于用WKB近似求解一量子系统中的相对应的问题的基本步骤,可由上述基本思想将之归结为以下的五个步骤:
第一步分析问题,将问题中涉及的波函数转变成相关的指数函数;
第二步是将所得到的相关指数函数运用于相关薛定谔方程中;
第三步将得到的指数函数中的参数转化成约化普朗克常量的幂级数;
第四步再按照不同次幂进行匹配,通过一一比对,得出相关的方程组;
第五步通过对各个方程的连理求解,最终得出波函数的近似形式并解决相应问题。
1.4 遂穿概率之转移矩阵法简介
转移矩阵法(Transfer Matrix Method)简称TMM,是一种分析解决有关波动方程问题的常用办法。因为薛定谔方程与波动方程具有一定程度的近似特征,因而能够在对粒子在势场中的运动问题进行讨论时,利用转移矩阵法的相关知识。由于用到的解决方法是通过利用转移矩阵得到相关的粒子隧穿概率谱以及反射概率谱,于是就将此种解决办法称为转移矩阵法。转移矩阵法具有很好的适用性,能够高效率地处理任意势垒中的粒子问题(即转移矩阵法既可以用于解决粒子在有规则的,简单的势垒中的隧穿问题;也可以用于解决粒子处于不规则且复杂的势垒中时的相关隧穿问题)。
第2章 运用WKB近似以及矩阵转移法求隧穿概率
2.1 引言
大量的研究计算表明,当研究普通且不规则的势垒时,由于没有办法得到准确的薛定谔方程,研究者们往往利用近似法来解决相关问题;而在时间推移科技进步下,计算方法得到进一步改进,矩阵转移法出现在人们视野中。下面将就具体问题对近似法和矩阵转移法进行简单比较。
2.2 WKB近似法求解简单三角形肖特基势垒隧穿概率公式
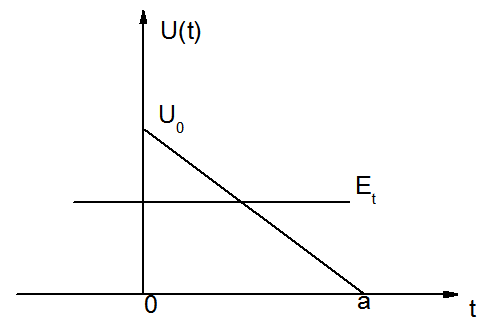
由于金属材料与半导体材料相互接触而构成的肖特基势垒,其形状取决于半导体材料内的掺杂情况,当掺杂分布为均匀型、高斯型以及指数型时,其所对应肖特基势垒形状各不相同,处理的复杂程度也不相同。下面只分析求解掺杂分布为均匀型时,对应的隧穿概率。
假设一三角形肖特基势垒的分布图可用下图表示:
剩余内容已隐藏,请支付后下载全文,论文总字数:15688字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;