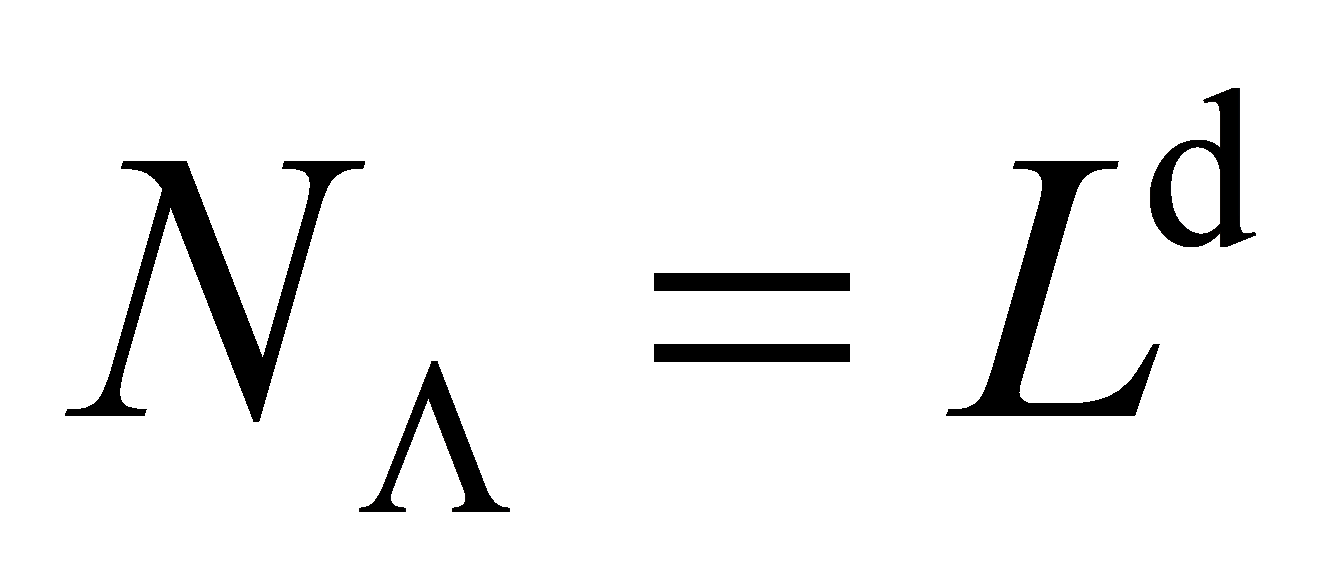论文总字数:12415字
目 录
1.引言………………………………………………………………4
1.1量子相关概念…………………………………………………………………4
1.2 国内外研究现状……………………………………………………………………5
2. 模型与量子相干……………………………………………………5
2.1XXZ模型和横向场XY模型的介绍……………………………………………………5
2.2量子相干有关公式的推导…………………………………………………………8
3. 讨论与结果…………………………………………………………11
3.1 单自旋的量子相干…………………………………………………………………11
3.2 双自旋的局部量子相干………………………………………………………………13
4. 论文总结………………………………………………………17
5. 附录………………………………………………………………17
参考文献………………………………………………………………20
致谢……………………………………………………………………21
XY链横向场中量子相干的尺寸效应
王大明
,China
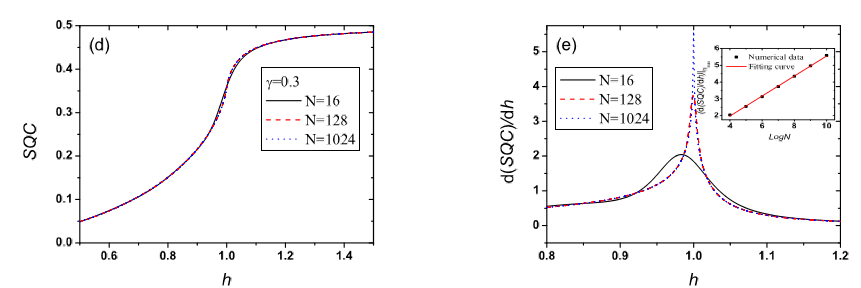
ABSTRACT: Based on the Winger-Yanase skew information, the size effect of the quantum coherence in the ground state of the finite transverse-field spin-1/2 XY chain is explored. It is found that the first-order derivatives of the single-spin coherence and the two-spin local coherence both have scaling behaviors in the vicinity of the critical point. A simplified version of coherence is also studied and the same characteristics with its counterpart are found.
Keywords: Quantum phase transition, Critical spin systems, Quantum coherence.
1、引言
1.1量子相关概念
量子叠加是量子系统十分重要的性质,也是量子相干,量子纠缠和其它量子关联必要的条件。现在对量子关联的基本原理和应用方面已经有了非常成熟的研究[1,2]。量子相变[3,4]是凝聚态物理领域里的一个非常重要的课题。基于对量子关联的明确定义以及最近快速发展的量子信息科学[5,6],通过量子信息理论观点研究量子相变已经在国际上引起了广泛的关注[7-16]。
自然界中,在处于基态的量子多体系统中存在着真正的量子转换,产生了物质性质不同的几个阶段。这种相变,纯粹是由于海森堡测不准原理造成的量子涨落,被称为量子相变。虽然量子相变在绝对零度的温度下发生系统不断变化的参数在临界点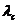 ,也可以观察到在足够低的温度下,热波动不足以激发系统的基态。量子相变与基态的能级交叉发生在量子多体的系统中,通常会导致基态能量的非解析性。特别是,一阶导数不连续的基态能量被公认为一阶量子相变,同样的,二阶导数不连续或者二阶导数发散是二阶量子相变的主要特征。在这种情况下,基态能量的一阶导数是连续的,另一方面,也有更多量子相变的类型,在这个标准框架内无法得到理解。
,也可以观察到在足够低的温度下,热波动不足以激发系统的基态。量子相变与基态的能级交叉发生在量子多体的系统中,通常会导致基态能量的非解析性。特别是,一阶导数不连续的基态能量被公认为一阶量子相变,同样的,二阶导数不连续或者二阶导数发散是二阶量子相变的主要特征。在这种情况下,基态能量的一阶导数是连续的,另一方面,也有更多量子相变的类型,在这个标准框架内无法得到理解。
量子自旋链存在着几种不同的量子临界现象,因此作为研究量子相变最主要的途径。此外,当系统处于外部横向磁场时,通过一个因式分解得到了另一个基本原理。这一现象被定义为在特定的磁场内存在一个完全因式分解的基态。即,在分解点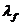 ,发生的分解现象已经证明在基态和双自旋量子相干的对称性发生了改变。量子系统具有真正的量子性质的相干性,是许多应用量子信息科学的基本原理。事实上,从许多不同的角度研究量子自旋链非常重要。
,发生的分解现象已经证明在基态和双自旋量子相干的对称性发生了改变。量子系统具有真正的量子性质的相干性,是许多应用量子信息科学的基本原理。事实上,从许多不同的角度研究量子自旋链非常重要。
半个世纪前,Winger和Yanase首次引入倾斜信息的概念[17-22],Winger和Yanase的倾斜信息理论对量子物理有几个非常有趣的解释在参考文献[17]中,它可以作为观察在一个量子态量子不确定性的量度。
量子纠缠,作为展示纯量子不同系统之间的关系的量度,已经成为量子力学的局部内涵之外的标志之一。 最近,许多物理学家们在努力理解在一些在多体的基态自旋模型里的量子纠缠, 目的之一就是我们希望通过一个彻底的研究这些系统里的量子纠缠从而得到对这些系统中的量子相变一些新的发现。例如,Osterloh等研究了在横向磁场伊辛模型中两个最近自旋的量子比特间量子纠缠的并协度,他们发现,这个系统的并协度显示出奇点并且遵守在量子相变点附近的标度律。另一方面,对于其他模型,如反铁磁性的XXZ链则表现出完全不同的并协度。并协度是一个各向异性参数连续函数,并且可以达到一个最大的过渡点。因此,在这两种情况下,可以观察到并协度本身会在量子相变点产生令人感兴趣的现象。然而,我们应该强调的是,这种行为本身可能并不总是意味着量子相变。他们广泛的研究了在反铁磁性的XXZ链的近邻自旋量子纠缠。通过提供解决方案中拟设模型的结果,我们可以清楚的显示出这个系统中近邻自旋的的量子纠缠的并协度是一个各向异性耦合参数的连续函数,并且在在各向同性海森堡格点达到最大值。
1.2国内外研究现状
最近,几个包括矩阵范数,保真度和相对熵的精确测量,用于量化一个给定量子态的量子相干的方法已经在不同的模型中得到了应用[17-19]。基于Winger和Yanase 引入倾斜信息的概念,参考[23]我们发现在热力学极限下,横向场XY链基态的量子相干为研究模型的量子相变提供了重要的一些信息。另一方面,其它现已知[9,11]的相关测量,比如对量子纠缠的同时测量[24],Zurek[25]在对量子失谐的研究中发现链的尺寸在临界点的对数有发散性。但是,在量子相变模型中在临界点的量子相干的尺寸效应目前我们仍然不清楚。
在本篇文章中,基于参考[23]我们将在基础上深入研究横向场XY模型中量子相干的尺寸效应。我们数值模拟了在量子相变模型临界点附近量子相干的扩展行为,我们发现单自旋相干和双自旋局部相干的一阶导数的奇异点相同,那就是说,即不同的拟合系数给出了线性对数发散或者平方对数发散。此外,简化的量子相干的模型实验结果良好,而且发现了相似的结果。
文章分为这样几个部分,第二节介绍了相关的模型和公式,以及简略的阐述了量子相干的概念。第三节是我们得到在有限的模型中对量子相干数值模拟的结果。最后一节,我们给出了结论。
2、模型和量子相干
2.1XXZ模型和横向场XY模型的介绍
在表达式中 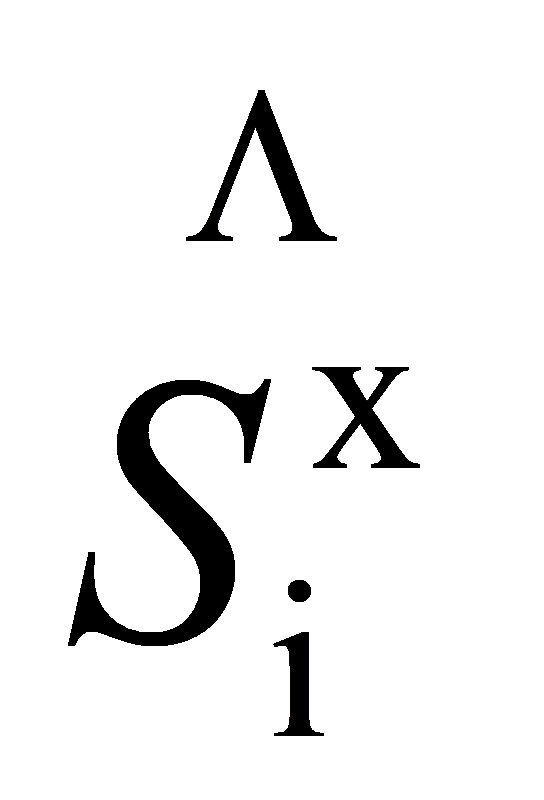 ,
,
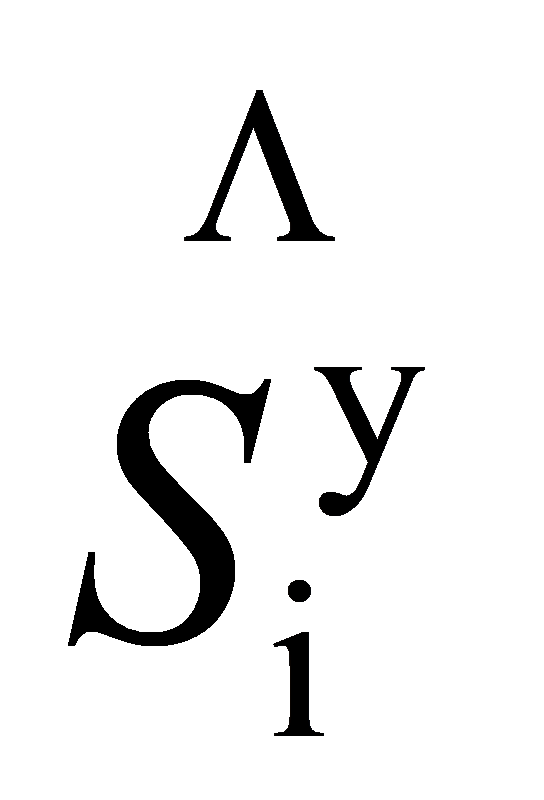 和
和 是1/2自旋运算符和是一个无参数描述的各向异性模型。哈密顿量的总和超过成对的I和J明显的,哈密顿量总是与Z分量运算符进行交换。因此,每个哈密顿量也是一个本征态
是1/2自旋运算符和是一个无参数描述的各向异性模型。哈密顿量的总和超过成对的I和J明显的,哈密顿量总是与Z分量运算符进行交换。因此,每个哈密顿量也是一个本征态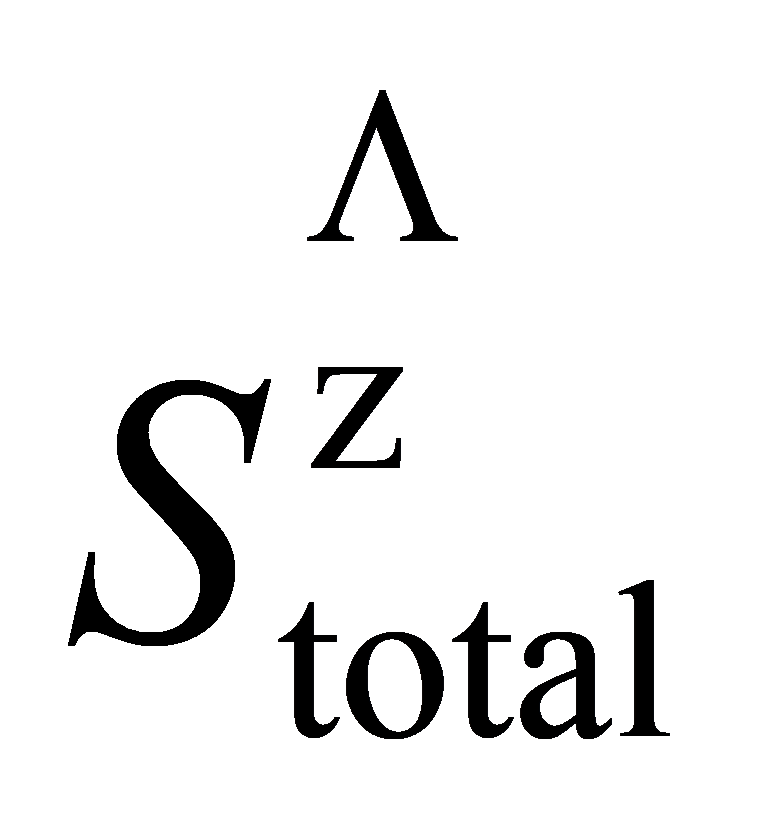 。从而,系统的变换空间可以分解成许多子空间V,在每个子空间中,自旋量子数
。从而,系统的变换空间可以分解成许多子空间V,在每个子空间中,自旋量子数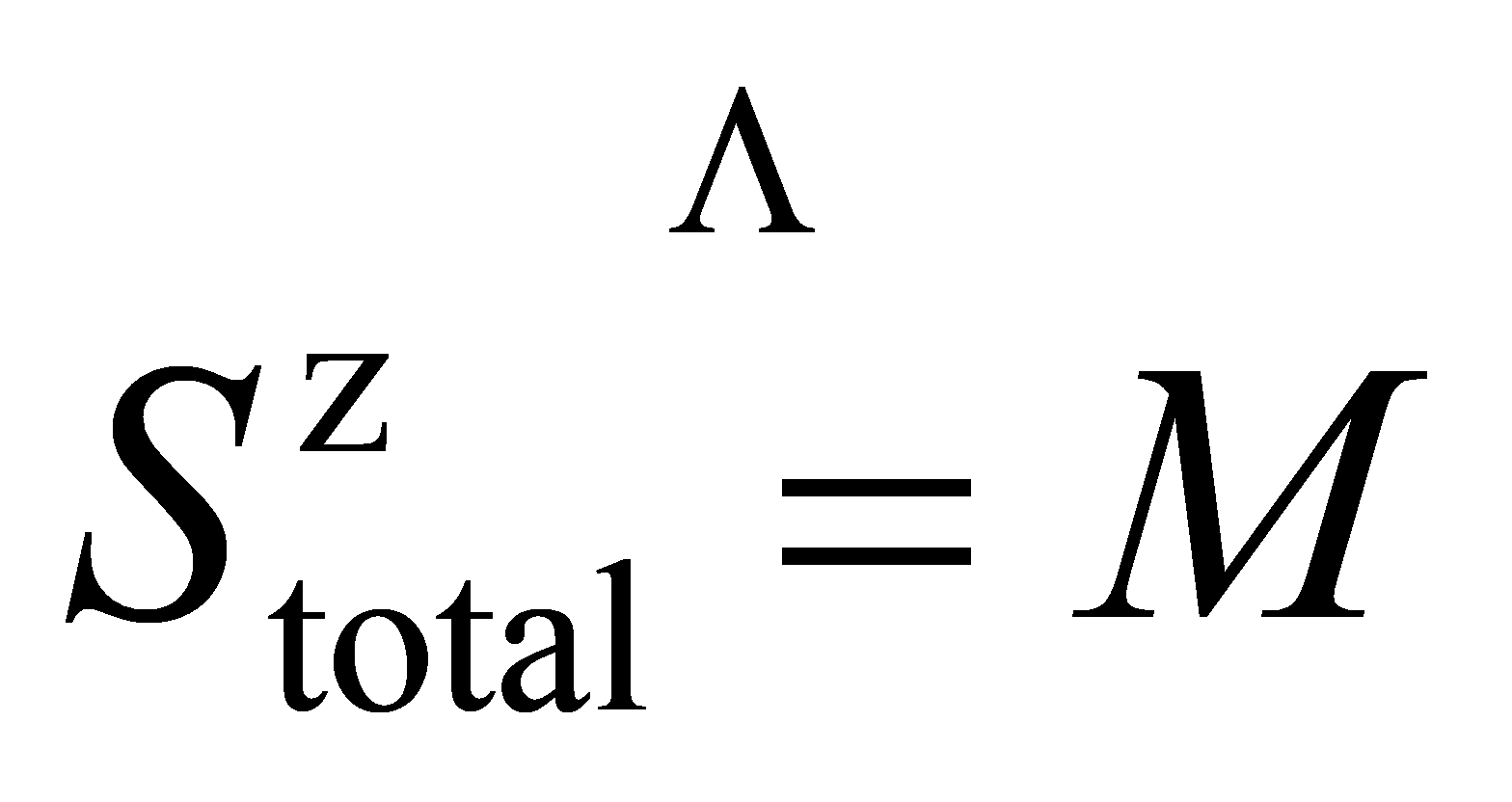 是指定的。众所周知,在一个有限的简单立方晶格A中,XXZ模型非简并的基态允许任何子空间V(X)。特别是,其总基态
是指定的。众所周知,在一个有限的简单立方晶格A中,XXZ模型非简并的基态允许任何子空间V(X)。特别是,其总基态 在子空间中与基态相符的V(M=0)。也存在非简并,因此,所有的物理量,例如基态能量
在子空间中与基态相符的V(M=0)。也存在非简并,因此,所有的物理量,例如基态能量 和自旋相关函数是解析函数的参数
和自旋相关函数是解析函数的参数 ,只是晶格是有限的。
,只是晶格是有限的。
同时 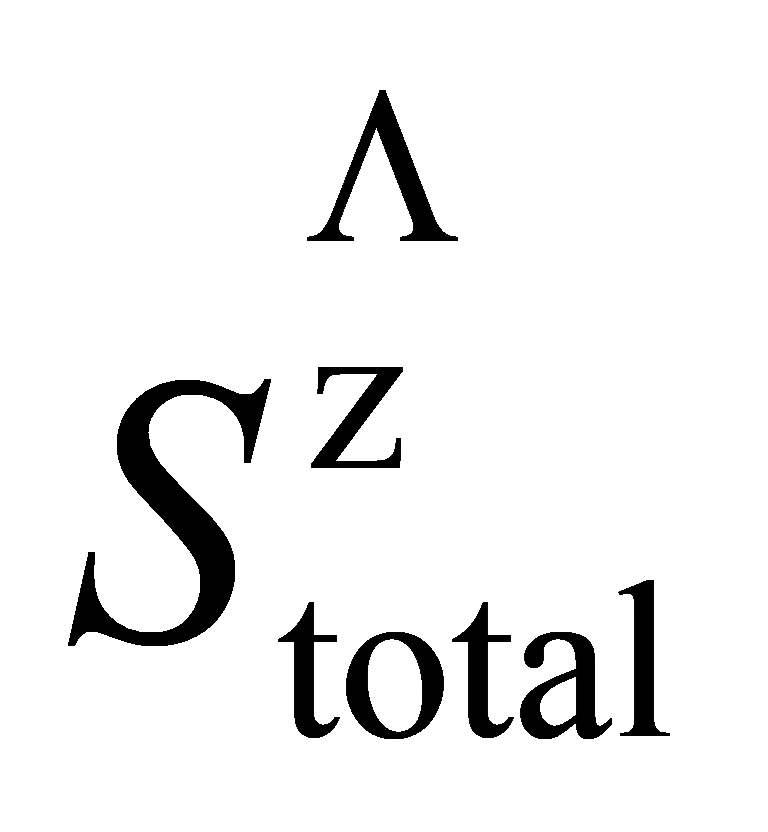 也意味着,遵守标准的基向量 |↑↑
也意味着,遵守标准的基向量 |↑↑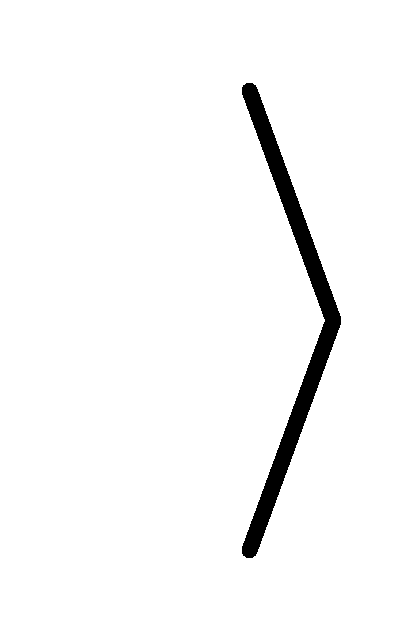 , |↑↓
, |↑↓ , |↓↑
, |↓↑ 和|↓↓
和|↓↓ ,由一对临近的晶格格位I和J放在区域对角化的密度矩阵:
,由一对临近的晶格格位I和J放在区域对角化的密度矩阵:
两个旋转同时发生的相关函数,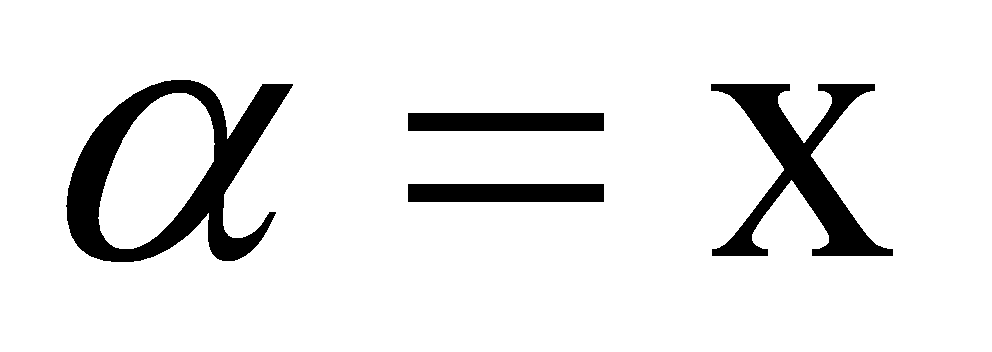 ,y,z,它可以写成
,y,z,它可以写成 ,由变分原理,可以得到所有自旋关联函数
,由变分原理,可以得到所有自旋关联函数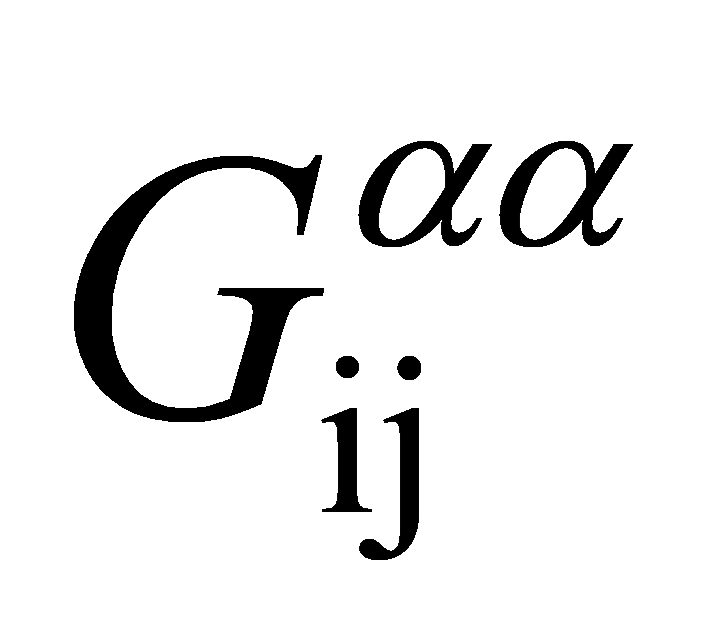 是负的。得到:
是负的。得到:
这里在晶格中数量),是基态能量密度,此外,由于所有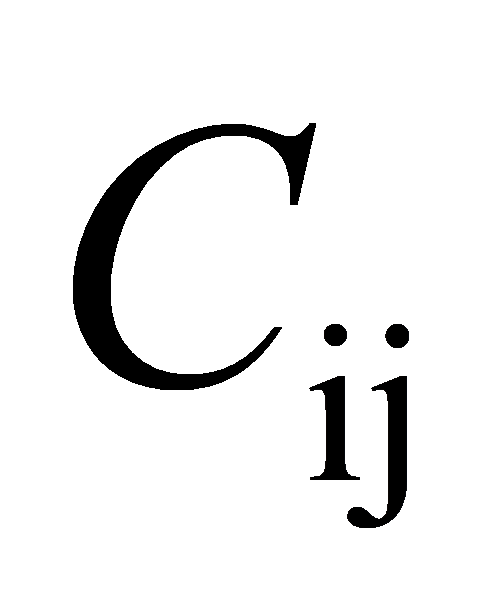 是解析函数的参数,允许对
是解析函数的参数,允许对 求导,特别是对
求导,特别是对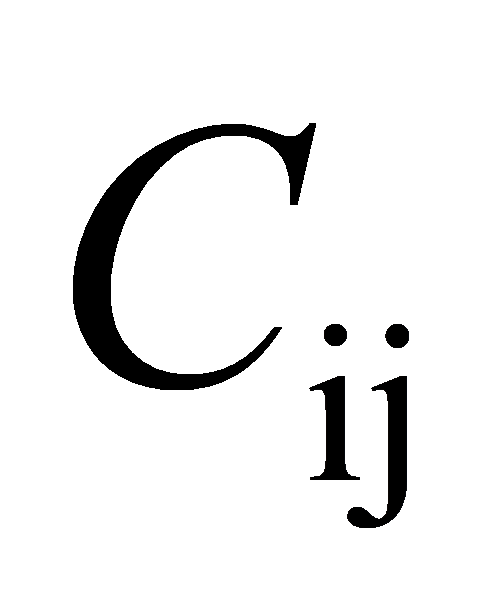 的一阶导数,得到了:
的一阶导数,得到了:
,
剩余内容已隐藏,请支付后下载全文,论文总字数:12415字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;