论文总字数:15656字
目 录
一、 引言 5
二、 理论基础 6
2.1应力和应变 6
2.2应力与应变之间的物性关系 7
2.3切应力互等定律 8
2.4静距和惯性矩 8
2.5梁的挠度与转角 8
三、弯曲正应力 9
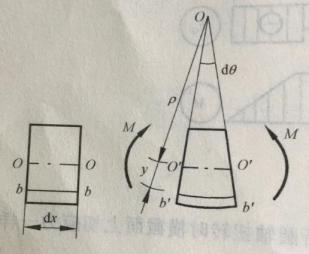
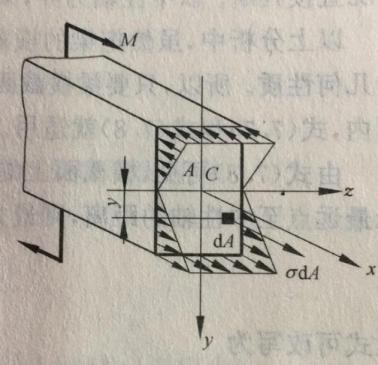
3.1纯弯曲梁的正应力 9
3.2横力弯曲梁的正应力 13
四、弯曲切应力 13
4.1矩形截面梁 13
4.2工字型截面梁 15
4.3圆形截面梁 18
4.4开口薄壁截面梁 20
五、 切应力对梁的形心位移(挠度)的影响 22
5.1切应力对矩形截面梁挠度的影响 22
5.2切应力对工字型截面梁挠度的影响 24
5.3切应力对圆形截面梁挠度的影响 26
5.4切应力对开口薄壁截面梁挠度的影响 28
六、结论 29
参考文献: 31
致谢 32
横向弯曲下梁切应力的探讨
徐保君
,China
Abstract:In the case of transverse bending, there is not only normal stress but also shear stress on the cross section. However, in some projects, there are beams with short spans and high cross-sections, thin beams with ventral plates, and so on.The bending shear stress of the beam may reach a very high value, so the bending shear stress must be calculated. In this paper, the distribution of shear stress of different types of beams is discussed, and the influence of shear stress on beam deflection(displacement) is considered, and the correction value of deflection is calculated quantitatively.
Key words:Material mechanics;Shear stress; Horizontal bending;Cantilevered beams; deflection
- 引言
在改善生活、征服自然、改造自然的活动中,人们往往不得不建造各种建筑。任何建筑物(液压建筑、工业和民用建筑、桥梁隧道等)都是由根据某些法律合并而成的许多零部件组成的。这些部分被统称为组件。
根据构件的主要几何特征,可分为几种,其中一种称为杆,是材料力学研究的主要对象。
杆的几何特征是长度l比横向尺寸(高为h,宽为b或直为d)大得多。它的轴(与截面中心的连接)是一条直线,定义为直杆;曲线的轴曲杆是曲线的轴。截面有变化的杆可变截面杆是有截面有变化的杆;截面无变化的直杆相等的直杆是有截面无变化的直杆。
当建筑物承受到外力的作用(或其它外在因素的影响)时,组成该建筑物的各杆件都必须能够正常地工作,这样才能保证整个建筑物的正常工作。为此,要求杆件不发生破坏。如建筑物的大梁断裂时,整个结构就无法使用。不破坏并不一定能正常工作,如果杆件受到外力的作用变形太大,就会影响正常工作。如果起重机梁因负荷过大而变形过大,则会影响起重机的正常行驶。举另一个例子,如果机器的主轴弯曲太大,就会引起振动,影响机床的质量。此外,在载荷作用下还存在一些杆件,其所有的平衡形式都可能失去稳定性。举个例子,假设压力柱又细又长,它可能在受到压力作用后超过一定极限后显著弯曲变形。直柱受压突然变弯,这一现象称为丧失了稳定性。杆件失稳将造成类似房屋倒塌的严重后果。总而言之,杆件要能正常工作,必须同时满足以下三方面的要求:
(1)不会发生破坏,即杆件必须具有足够的强度。
(2)不产生过大变形,发生的变形能限制在正常工作许可的范围以内,即杆件必须具有足够的刚度。
(3)不失稳,杆件在其原有形状下的平衡应保持为稳定的平衡,即杆件必须具有足够的稳定性。
这三方面的要求统称为构件的承载能力。一般来说,在设计每一杆件时,应同时考虑到以上三方面的要求,但对某些具体的杆件来说,有时往往只需考虑其中的某一主要方面的要求(例如以稳定性为主),当这些主要方面的要求满足了,其它两个次要方面的要求也就自动地得到满足。
当设计的杆件能满足上述三方面的要求时,就可认为设计是安全的,杆件能够正常工作。一般说来,只要为杆件选用较好的材料和较大的几何尺寸,安全总是可以保证的,但这样浪费材料、空间和金钱。显然,过分地强调安全可能会造成浪费,而片面地追求经济可能会使杆件设计不安全,这样安全和经济就会产生矛盾。材料力学正是解决这种矛盾的一门科学。在材料力学知识的基础上,可以了解如何在安全的条件下最大限度地降低钢筋零件的材料消耗。正是由于这一矛盾的不断出现和不断解决,材料力学才不断发展。
为了能既安全又经济地设计杆件,除了要有合理的理论计算方法外,还要了解杆件所使用材料的力学性能。固然有的材料的力学性能从有关手册中可以找到,但是有的情况下还必须自己测定,因此还必须掌握材料力学的试验技术。通过杆件的材料力学试验,一方面可以测定各种材料的基本力学性质;另一方面,对于现有理论不足以解决的某些形式复杂的杆件设计问题,有时也可根据试验的方法得到解决。故试验工作在材料力学中也占有重要的地位。
近代物理学的研究指出一切物体是由不连续的微粒组成的,它们的规则或不规则地排列着,相互间同时存在吸引力和排斥力并保持平衡。若要根据这样复杂的物质构造来研究构件的抗力能力,即使可能也是及其困难的。为了得出简便切实的结论,我们对构件组成体做出如下的基本假设。
连续性假设:这一假设认为,材料是填充的几何体积的整个物体没有间隙,它的结构是紧凑的。虽然变形的固体在物质结构上有不同程度的空隙,但在微观水平上并不是连续的。然而,与组件的大小相比,这些空洞非常小,因此可以忽略不计。因此,可以认为材料在整个几何体积中是连续的。
均匀性假设:该假设认为物体内各处的性质均完全相同。如果人体的任何部分被截获,无论其大小和位置如何,其机械性能是完全相同的。然而,材料力学研究的元件(或截获的零件)包含无数的晶粒,它们是随机排列的。它的力学性质是所有晶粒性质的统计平均值,因此从宏观上可以认为各组分的性质是一致的。
各向同性假设:假设是物体在各个方向都具有完全相同的力学特性。具有这一特性的材料称为各向同性材料。在工程中常用的金属,就其单粒而言,具有方向性的机械性能。在不同的方向上,它们的力学性能并不相同,但是物体包含了非常多的晶粒。谷物排列不规则,每个方向都具有相同的性质。各向异性材料的定义是在各个方向具有不同力学性能的材料。
小变形条件:在材料力学的研究中,构件在外力作用下的变形通常与构件的原始尺寸相比非常小,可以看作是一种数学上的痕迹。因此,当考虑一个成员的平衡或移动时,它的变形可以省略。根据变形前的初始尺寸,计算受力分析。
- 理论基础
2.1应力和应变
应力就是分布内力在某一点上的集度。通常来说,截面上附加的分布内力总是可以分解成两种类型:作用线垂直于截面的应力称为正应力,用字母 表示;作用线位于截面内的应力称为切应力,用字母
表示;作用线位于截面内的应力称为切应力,用字母 表示。
表示。
绕着受力的弹性体中随机点选取微元体(一般情况下为正方体),通常情形下,应力作用在微元体的所有面上。接下来考虑两种最容单的情况
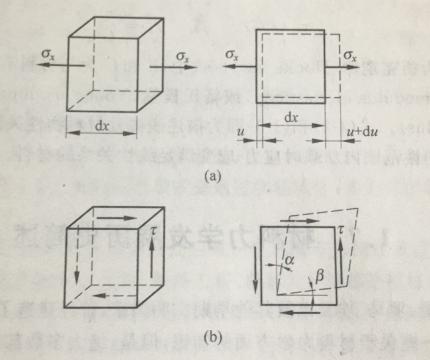
图2-1 正应变与切应变
对于正应力条件下的微量元素(图a),沿正应力方向会发生伸长和缩短,并垂直于正应力方向。这种变形称为线性变形。描述弹性体在每一点的线性变形程度的量称为正应变或线性应变 。根据微量元素变形前后
。根据微量元素变形前后 方向长度
方向长度 的相对变化,有
的相对变化,有

在公式中,微量元素在变形前的长度 方向是正应力作用;
方向是正应力作用; 是微量元素在变形后沿正常应力方向的两个截面的相对位移。
是微量元素在变形后沿正常应力方向的两个截面的相对位移。 下标
下标 表示应变方向。
表示应变方向。
剪切应力的作用会使微元体产生剪切变形,而微量元素直角的变化可以测量剪切变形程度。微元件直角的变化数称为剪应变或剪应变,并用 表示。在图b中,
表示。在图b中, ,单位为rad。
,单位为rad。
2.2应力与应变之间的物性关系
剩余内容已隐藏,请支付后下载全文,论文总字数:15656字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


