强子对撞中的轻子对产生

论文总字数：27444字

摘 要

本文主要研究了质子-质子碰撞过程中的轻子对产生过程，即Drell-Yan过程。Drell-Yan过程探测强子内部结构，以及检验强相互作用的基本理论——量子色动力学(QCD)的一个基本过程。在因子化(factorization)的框架下，该过程可以通过某一能标，被划分为低能非微扰的部分，以及高能硬散射部分。过程的截面可以表达为这两部分的卷积。

Drell-Yan过程的最低阶硬散射过程是分别来自于对撞质子的夸克和反夸克对湮灭为虚光子，然后由虚光子产生正负电子(或muon子)对。最低阶过程的理论分析已经比较透彻。

本项目的可行性在于对因子化定理的合理运用。因子化定理保证了该过程是可以计算的，且可以得到物理的结果。在因子化框架下，低能非微扰的部分是不可计算的，但是是普适的不依赖于过程的，即可以参数化为普适的部分子分布函数，且一个过程中测量到的结果可以运用到另外一个过程中。高能硬散射过程依赖于具体的初末态粒子，但是由于强作用的耦合常数在能量高时较小，因此硬过程是可以做微扰展开计算的。

关键词：Drell-Yan过程，部分子模型，重整化，领头阶修正

HADRON COLLIDER TO PRODUCE THE LEPTON PAIR

Abstract

This paper studies the proton - proton collisions in the lepton pair production, which called Drell-Yan process. Drell-Yan process probe the internal structure of hadrons, and is a fundamental process to test basic theory of the strong interactions - quantum chromodynamics (QCD). In the framework of factorization, This can be done through an energy labeled, it is classified as low-energy part of nonperturbative and hard scattering of high-energy part. Cross-section of the process can be expressed as the convolution of this two parts.

Minimum order hard scattering process of Drell-Yan process is from the collision of protons are quarks and anti-quark pair annihila-tion of virtual photons, Then virtual photon produces electron-positron pairs(or muon). Theoretical analysis of the lowest order processes is thorough.

The feasibility of the design is the rational use of the factorization theorem. Factorization theorem guarantees that the process can be calculated, and we can get physical results. In the framework of factorization. Low energy nonperturbative part is incalculable. But it is not dependent on the universal process, so It can be parame-terized universal parton distribution functions. And one process measured results can be applied to another process. Energy hard scattering process depends on the specific initial and final state particles. However, due to the strong coupling constant role in high energy is small, so hard process that can be done to calculate the perturbation expansion.

KEY WORDS: Drell-Yan process, parton model, renormalization, leading order correction

目录

摘要 1

Abstract 1

第一章 绪论 4

1.1 引言 4

1.2 夸克-部分子模型 4

1.2.1 强子的夸克模型 4

1.2.2 部分子模型 6

1.3 量子色动力学（QCD）理论的正则化和重整化 9

1.3.1 维数正规化 9

1.3.2 重整化 11

第二章 Drell-Yan过程 13

2.1 高能强子对撞：Drell-Yan过程 13

2.1.1 非极化的Drell-Yan过程 13

2.1.2 极化的Drell-yan过程 15

2.2 Born截面 17

2.3 PDF重整化 19

2.4 修正 21

第三章 结论 26

第四章 文章中所用到的数学工具 27

致谢 33

参考文献 34

第一章 绪论

1.1 引言

高能核子—核子相互碰撞的Drell-Yan反应的过程如下：两个入射核子相互碰撞，其中一个入射核子中的一个夸克和与他相撞的另一个核子中的一个反夸克湮灭，由此产生一个具有不变质量的矢量波色子（包括光子、Z波色子和W波色子）。紧接着，这个具有不变平方质量的矢量波色子将会分裂成一对具有质量的轻子对。当反应产生的矢量波色子为光子时，产生的轻子对可能是，当产生的矢量波色子为Z波色子或者W波色子时，产生的轻子对可能是e、或者

通过Drell-Yan过程，我们可以对强子中的夸克、胶子的分布、结构有更加深入的了解，同时我们也可以通过相关的实验来对量子色动力学理论做重要的试验。又由于轻子-核子的深度非弹性散射实验中只有电弱相互作用参与反应，而在强子-强子对撞试验中，粒子间的相互作用为强相互作用，因此我们也可以通过Drell-Yan反应过程来对强相互作用做更深入的了解，同时也能探测强子的结构性质。

1.2 夸克-部分子模型

1.2.1 强子的夸克模型

1932年查德威克发现了中子，紧接着，海森堡和伊凡宁柯分别各自独立提出了原子核是由质子和中子组成的模型。由此，人们对物质世界的构成又有了新的突破。整个物质世界都是由原子组成的，原子由在其中心占据极小体积却有其质量绝大部分的原子核及围绕原子核旋转的电子组成，原子核又由质子和中子组成。但是质子和中子是如何紧密结合在m的空间中的还是无法解释的疑问。1935年汤川秀树提出质子和中子是通过交换一种还未被发现的介子来结合在一起的。这种力是一种新型的作用力，即强相互作用。后来，人们发现自然界已发现的粒子可以分成三类：一类是参加强相互作用的粒子，被称为强子，如中子、质子、π介子。奇异粒子等，另外一类是不参加强相互作用的粒子，被称为轻子，如电子、μ子、中微子等；剩余一类是传递相互作用的粒子，被称为媒介子，如光子，中间玻色子和胶子。本项目研究的是强子（核子）—强子（核子）相互碰撞所产生的反应。

由于在强相互作用中质子和中子之间的相互作用与其是否带电无关，即电荷与强相互作用无关，同时如果忽略质子和中子之间微小的质量差异，那么质子和中子除了电荷不一样外其他的物理性质都是一样的。为了解释强相互作用的这种电荷无关性，在1936年，B.Cassen和E.U.Condon 提出了同位旋这一概念。通过引入同位旋，质子与中子可以被看成是同一种粒子—我们称之为核子N的两种不同的状态。在数学上，对同位旋的描述可以通过引入SU(2)群来完成。同位旋算符就分别对应SU(2)群中的三个生成元。

这里为泡利矩阵

由此可以得到同位旋算符满足下列对易关系

即角动量算符的对易关系‘

类似于自旋，可以得出同位旋T=，质子与中子就分别表示为同位旋T在同位旋空间里的两个本征态，即为核子的二重态，质子（）,中子(= -1/2)。

这样核子可以采用如下方式表示

，T=1/2 ,

对于π介子，其荷电和中性，三种π介子，，构成同位旋的三重态

，T=1

，

，

π介子，质子和中子都满足下列关系

Q=B/2

即电荷-同位旋关系。其中B为重子数，介子的重子数为0，质子，中子等其他重子的重子数为 1。

上述理论，特别是同位旋的引入很好的解释了核子的一些问题，但是随着实验技术的不断发展，更多的粒子不断被发现，在二十世纪六十年代初期，大量的强子被发现。其中有相当一部分的粒子的奇异量子数不为零。就像物理史上不断发生的那样，实验上新的进展需要新的理论加以解释，仅仅引入同位旋显然不足以将新发现的强子包含进去。对称性已经不足以解释强子模型，于是Gell-Mann和西岛将上述的电荷-同位旋关系扩展为

Q=Y/2 ，Y=B S

这一公式能很好的符合新发现的粒子。同时，做这样的扩展能很自然的将描述同位旋空间不包含奇异数的SU(2)对称性推广到包含奇异数的SU(3)对称性。按SU(3)对称群对已发现的强子进行分类，即以Y和这两个好量子数对强子进行分类，并取SU(3)群的秩为Y和。重子可以填充到八重态和十重态中，而介子可以填充在单态和八重态里。上面的理论虽然从数学上很好的符合了实验上的新的进展，但是具体的物理图像还是并不清晰，为此1964年，Gell-Mann和Zweig提出了夸克模型来对强子的构成做物理的解释。他们引入了三种新的并且是更为基本的粒子，他们将其命名为夸克。最初Gell-Mann和Zweig引入了三种夸克，分别对应于SU(3) 群的基础表示的三个基，即

其中u表示上（up）夸克，d表示下（down）夸克，s表示奇异（strange）夸克。强子可以按照夸克与SU(3)群基的对应关系看成是由这三种夸克组成。夸克模型认为三种夸克和他们的反夸克组成了所有的介子和重子。例如π介子，，，；质子p=(uud),中子n=(udd)。夸克模型可以很好地符合实验观察到的强子谱。根据夸克模型，介子由正反夸克组成，那么其自旋应为J=L S,其中S是正反两个夸克所组成的自旋，L是正反两个夸克的相对角动量。由此可以很容易的得出介子的电荷共轭宇称以及宇称，分别是，。

然而新的实验瘸却发现了一些新的粒子。1974年丁肇中和Richter发现了J/粒子。这种例子并不能由上述的夸克模型进行分类，后来发现J/粒子是由粲夸克和反粲夸克组成。其后1976年又发现了底夸克，1995年发现了顶夸克。上夸克(u)、下夸克(d)、奇异夸克(s)、粲夸克(c)、顶夸克(t)、底夸克(b)。这六种夸克便是标准模型中的三代夸克。其中u,d,s为轻夸克。c,b,t为重夸克。所有自然界的强子都是由这六种夸克和他们的反夸克组成，六种夸克可以按照其性质分成三组

，，

u,c,t的电荷为2/3,d,s,b的电荷为-1/3。

1.2.2 部分子模型

为了探明强子的内部结构，人们做了一系列的实验，其中1969年做的电子-质子深度非弹性散射得出了一个很有意思的结果，对于一个固定的（或者x）

，

强子的结构函数和在gt;1Ge的能量区域内存在所谓的标度无关现象，即以及不再是以和为变量的函数，而仅仅是的函数，而x并无量纲。即

由此可以得出一个等式

通过上述讨论可知，结构函数和仅仅是以x为变量的函数，而与无关。而x是一个无量纲的量，这恰恰表明结构函数与任意能量标度无关，这种现象称之为标度无关现象。标度无关现像的理论解释导致了部分子模型，而在试验中能量超过某一区域后标度无关现像会发生系统偏离，这一现象也可以从量子色动力学理论中的夸克-胶子相互作用理论来进行解释。

下面我们将解释如何从标度无关现像推至部分子模型。首先，当一个电子和一个点粒子发生弹性散射时，它的结构函数为

上面两个式子说明了当电子和另一个点粒子进行弹性散射时，这一过程对结构函数的贡献以及仅仅是的函数，即只是x的函数。

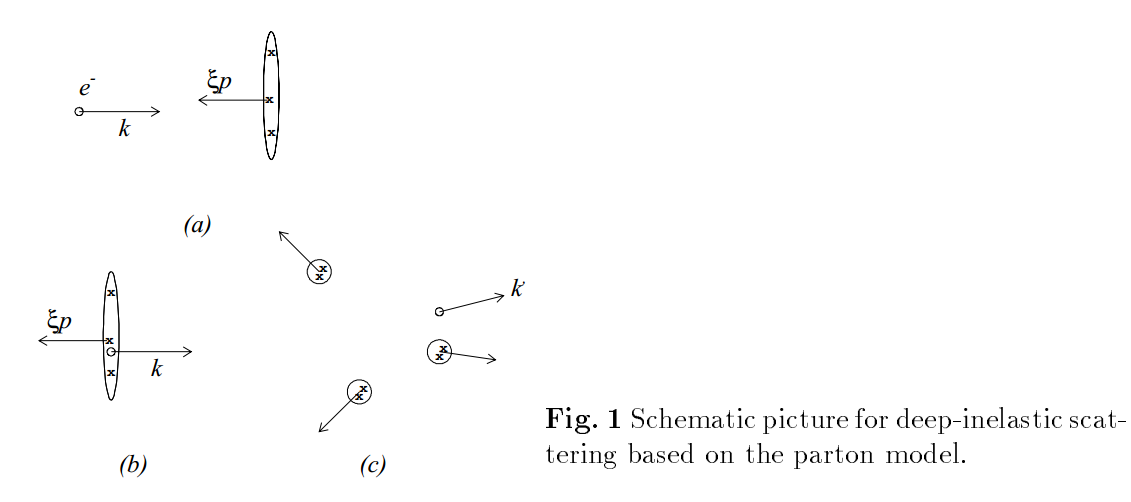有了上面这样一个结果，我们就能很容易的设想如果质子内部是由很多类似点粒子的成分组成，而电子和质子的非弹性散射是由许多电子-点粒子弹性散射过程组成的，那么电子-质子深度非弹性散射的标度无关性现象就很容易解释了。这些类似点粒子的成分我们称之为部分子。

下面就对部分子模型做一个简单的介绍。首先假设在无穷大动量系质子内的每一个部分子的四维动量都仅带总四维动量的一个分量，即

假设部分子的质量以及横动量可以忽略，那么在电子-质子非弹性散射中，电子-部分子不相干弹性散射对结构函数所作的贡献为

式子中，i代表质子中的部分子，代表第i个部分子的电荷，是指在动量分量处在区域内发现第i个部分子的概率。为了可以计算电子和部分子的弹性散射截面，先假设部分子为自旋为1/2的粒子。定义

且

W是终态所有强子的有效质量。由此，电子-部分子弹性散射截面就可以表示为

假设部分子之间是准自由的，那么将所有电子-部分子弹性散射截面叠加起来就能得到电子-质子深度非弹性散射截面。

剩余内容已隐藏，请支付后下载全文，论文总字数：27444字

相关图片展示：