论文总字数：22167字

目 录

1.绪论 1

1.1 研究背景及意义 1

1.2 Lipschitz非线性系统状态观测器的国内外研究情况 1

1.3 MATLAB 2

1.4本文的目的及主要工作 3

2.预备知识 3

2.1数学基础 3

2.2非线性系统观测器 4

2.3稳定性基本理论 6

2.4线性矩阵不等式（LMI） 9

3.非线性Lipschitz系统观测器设计 10

3.1系统描述 10

3.2 非线性状态观测器设计 11

3.3仿真算例 15

3.4本章小结 19

4.在非线性微分代数系统中的扩展 19

4.1系统描述 19

4.2状态观测器设计 20

4.3仿真算例 22

4.4本章小结 26

5.结论与展望 26

致谢 28

附录 29

非线性Lipschitz系统的状态观测器设计及其扩展

黄飞

Abstract:This paper studies the state observer design method for nonlinear systems which satisfies Lipschitz condition and its extension to nonlinear differential algebraic systems.By studying the observer gain matrix method based on algebraic Riccati equation design method and considering the inconvenience of solving algebraic Riccati equations which need to constantly adjust the parameters, linear matrix inequality is used to improve the selection method of state observer gain matrix.The simulation results show the effectiveness of state observer gain matrix that is constructed by linear matrix inequalities,which is less conservative than the method based on algebraic Riccati equation and can be solved more easily.

Keywords:Lipschitz，nonlinear system，state observer，linear matrix inequalities

1 绪论

1.1 研究背景及意义

在当今实际的社会生产生活中，我们经常能够看到的系统多半都是非线性系统，系统非线性的特征主要体现在以下几个方面：首先是由于系统的相对不完善所造成的非线性而使之产生，就例如我们常见的随动系统是用齿轮进行传动，传动的齿轮与齿轮之间由于生产工艺的原因难免存在齿隙和干摩擦等，我们常见的绝大多数的执行机构都很难做到毫无限制地加大它输出的功率，从而产生非线性。其次是由于系统本身的动态特性所造成的，就例如正在高速运转的机械手的关节与关节之间存在着哥氏力的耦合，像这样的耦合就属于非线性的，因此当我们在研究机械手的高速运转的控制工作前我们就一定要先考虑到非线性的耦合这种影响因素的存在。最后是想要把一些原本就是线性的对象进行相对较高的质量的控制工作，我们在一般情况下会有意在控制系统中加入非线性系统的相关控制原理。综上所述，对于非线性系统控制的问题很自然的就会变成大家十分关注的问题中的重要的一部分。也正是由于这些原因，越来越多的的非线性的相关的各种研发工作也成为了热点，各种新的技术手段也涌现了出来^[1]。

而状态反馈在有关于系统控制的各种综合问题中已经充分展示出了它的优越性。现在，人们往往总是会第一个想到利用状态反馈这种方式来解决系统的极点配置、镇定、解耦控制、无静差跟踪等各种类似的问题。然而通常情况下会因为系统的各种状态很难被简单的通过直接测量的方式来获得，又或者是因为测量所使用的设备常常也会受到一些经济上或是使用上的各种限制，从而使得我们很难在实际的生产过程当中得到系统的所有的状态变量，也使得我们很难得到状态反馈方式下的物理实现功能。这就造成了一个很大的矛盾，那就是状态反馈这种方式在其性能上不可替代，而其在物理上又存在着很大的不可实现性所带来的矛盾。在这样的情况下唯一能解决这种问题的方式就是状态重构^[2]。我们常常提到的状态重构的相关问题，总的来说就是设计观测器问题，我们简要来看就是运用重构系统的状态这种方式，并且将这个重构出来的状态用以替代系统实际的状态，运用这样的方法来呈现我们所需要的能够处理的状态反馈。如果具体的来说状态重构问题，其实就是在原有的系统之上重新构成一个新的系统，是用原来的系统当中能够是用直接测量的方式所得来的信息(比如说输入或者是输出)当作这一新构成的系统的输入信号，然后在设计好的条件之下让它的输出信号就相当于原来的系统的状态。于是像这样重新构造的新的系统我们就称它为状态观测器^[3]。

正因为在许多情况下，系统的状态往往难以全部获得，系统输出是唯一可用于反馈控制设计的量测信号，因此系统状态观测问题显得尤为重要。在实际应用中，许多系统具有非线性Lipschitz系统的形式，本文将研究此类系统的状态观测器设计问题，并将其扩展应用于更为广泛的非线性微分代数系统。本文对该类系统的研究具有一定的理论和实际意义。

1.2 Lipschitz非线性系统状态观测器的国内外研究情况

最初的Lipschitz非线性系统的状态观测器出现在二十世纪七十年代，经过几十年来的不断发展与完善，其在现实生活以及社会生产中的作用已经愈加明显。设计同类观测器已经成为了近年来热门的新课题，许多国内外学者争相研究，而他们的理论研究成果也进一步促进了观测器设计技术的成熟^[4]。

发展到现在，Lipschitz非线性系统状态观测器的种类也越来越多了，总的来说可以大致这样来进行分类：从时间角度来看，观测器分为可以对离散时间的观测^[5]以及对连续时间的观测^[6]这两种；而从状态结构角度来看，观测器又分为考察全维状态^[7]与降维状态^[8]两种不同的结构。

现在关于状态观测器的设计方法主要有两种。我们首先讨论第一种方法即Lyapunov方法^[9]。Lyapunov方法因其理论研究的深入透彻而受到广大研究者的青睐，然后此类方法也存在一些不足。其中较为明显的是Lyapunov方程或者Riccati方程的引入，这意味着需要求出正定解，而求解过程相当繁琐。尤其是对于Riccati方程，在求解正定解的过程中无法准确判定Hamilton矩阵中分块矩阵Q的正负性质，而这一问题，在现如今的国内外控制理论领域仍是一个未被解决的问题。其次运用这类方法虽然可以得到渐进收敛的结论，但是所获得的结论并没有直接意义。对于分块矩阵正负性的讨论，常见做法有两种：（1）通过计算Riccati方程来求得增益矩阵。这样比较直接但计算量过大^[10]；（2）采用LMI技术，人为地去构造增益矩阵，这种方法在实际中运用的较多，因为它相对便捷，而且MATLAB软件中本身带有LMI工具箱，可以方便有效的求解增益矩阵。

再讨论第二种方法，设计相应的状态方程。这种方法本质上来看是去计算得到误差动态方程，以此来证明设计的观测器趋向稳定。其优点是：求解过程本身较为直观，思路也容易让人理解，从误差动态的差分方程本身来看待问题。但也存在不足：增益矩阵的计算较为繁琐，通过状态方程来求解使得增益矩阵需要通过其他方式来间接得到。

1.3 MATLAB

MATLAB是本文的仿真算例所用到的最重要的工具。MATLAB又叫矩阵实验室，用英文来表达就是Matrix Laboratory，即是由Matrix和Laboratory两个单词结合而成。MATLAB公司已经发展了三十多年，MATLAB早已不是最初那个只是用于矩阵计算的软件了，如今的MATLAB包含了各种功能以及程序模块，其中就有十分先进的计算机编程的功能以及非常人性化的绘制仿真电路图的功能。正是由于如今的MATLAB软件使用起来极其方便，所涉及到的编程语言简单易学，数据处理函数别具一格，用户界面十分友好，极具人性化的特点，才使其在众多工程领域都广受好评，并且编入教科书，成为全世界各大高校学子所热衷且必须掌握的基本教学工具。

Simulink是MATLAB软件中十分重要的一个模块，他能简单有效地帮助我们对系统的数据模型和仿真结果进行分析。尤其在进行仿真电路图绘制的时候其界面显得尤为人性化，而且操作简单易学。你需要什么元件，只需要在左边工具栏中找到相应得找到该元件然后用鼠标拖动过来即可，如果需要设定或更改某些元件的参数，直接双击该元件进行参数的设定或更改就可以，然后将这些元件按要求连接就能得到你想要的仿真电路图。

本文使用了MATLAB软件中的LMI工具箱（LMI在下文的2.4中会进行具体介绍）和一些简单的程序编写和函数。下面结合本文所研究的系统对本文所涉及的程序以及PLOT函数作出示例：首先建立一个M文件，里面保存的是本文所研究的系统以及状态观测器的模型。然后再主程序里键入时间等参数有，调用M文件的函数以及PLOT函数进行画图。

例如:

t=[0,10];

x0=[1;-2;4;-3;3;0];

[tt,xx]=ode45(@DxDtY,t,x0);

figure

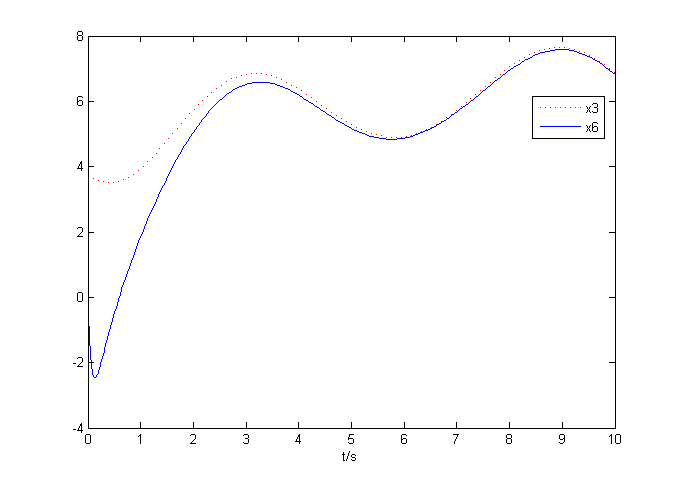
plot(tt,xx(:,3),'r:',tt,xx(:,6)) %建立图形

legend('x3','x6'); %标识图形

通过对MATLAB的了解，使我能够熟悉的应用MATLAB软件，并对我论文中的仿真工作起着重要的作用。

1.4本文的目的及主要工作

剩余内容已隐藏，请支付后下载全文，论文总字数：22167字

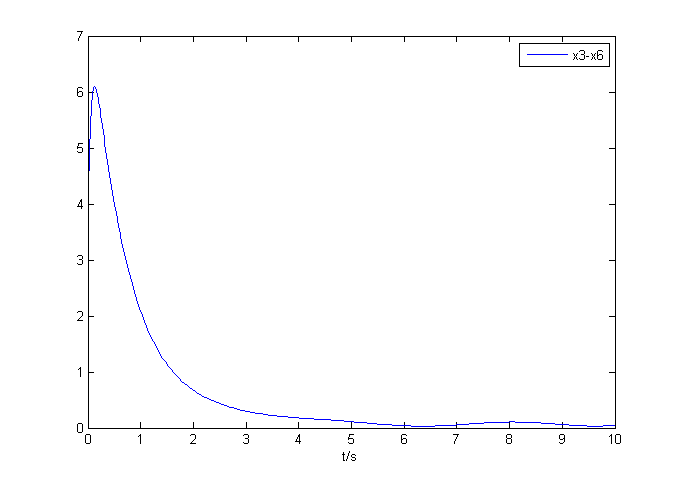
相关图片展示：