论文总字数:24486字
目 录
1 绪论 1
1.1 研究背景及意义 1
1.2 研究现状 1
1.3 主要工作 2
2 预备知识 2
2.1 微分代数系统 2
2.2 非线性系统 3
2.3 Lyapunov稳定性定义 3
2.4 Lyapunov稳定性判据 4
2.5 同步发电机组三阶模型 5
3 反步控制 6
3.1 一般系统的反步控制 6
3.2 三阶系统数值例反步控制 8
3.3 本章小结 11
4 同步发电机的非线性汽门控制设计 11
4.1 同步发电机汽门控制系统模型 11
4.2 同步发电机汽门控制设计 12
4.3 汽门控制系统仿真 14
4.4 本章小结 18
5 同步发电机的非线性励磁控制设计 18
5.1 同步发电机励磁控制系统模型 18
5.2 同步发电机励磁控制设计 19
5.3 励磁控制系统仿真 20
5.4 本章小结 22
6 结论与展望 23
6.1 结论 23
6.2 展望 23
参考文献 24
附录 26
基于微分代数系统的同步发电机非线性反步控制
孙帅
, China
Abstract: In this paper, we introduce a parameter estimation and use the backstepping control method to design a nonlinear controller for the differential-algebraic system with unknown parameters without interference. The designed controller can eventually make the synchronous generator closed-loop system asymptotically stable. Then, based on MATLAB software, the function simulation is carried out to simulate the synchronous generator control system in this situation to verify the correctness and validity of this method.
Keywords: differential-algebraic system; nonlinear backstepping control; synchronous generator;Matlab
1 绪论
1.1 研究背景及意义
从20世纪中期以来,我国工业水平不断提升的同时,电力工业的规模也在不断扩大,电力系统在生活与生产中的运用也在不断加强。随着科技的不断进步,我国电力系统的构造也与时俱进,复杂性越来越高。超远距离高压输电的技术在确保用电更加方便的同时也极大干扰了电力系统的稳定性,一旦超过电网所能承担的极限,整个电力系统便很可能产生各种故障。如果电力系统运行不稳定,就有可能造成大面积的停电,不仅会对生产生活造成不便,还会使得国家的经济产生不可估量的重大损失。基于上述各种原因,改善电力系统的稳定性是当前我国在电力系统运行方面需要不断进行的研究。
自上个世纪中期以来,线性系统的概念在理论研究上得到了逐渐完善,同时在各种各样的工业控制问题上也得到了成功运用。现代工业中,随着相关理论实际的不断发展,对控制系统的性能要求也不再简单,而是不断提高。传统的各种线性反馈控制理论已经不适合越来越复杂的工业控制问题[1],这是由于很多实际控制系统往往都不是线性而是非线性的。对于很多非线性现象,线性系统很难解释。而人们十分熟悉的电力系统就是非常典型的非线性系统[3]。在数学和物理科学中,非线性系统是输出变化与输入变化成正比的系统,非线性问题是工程师,物理学家和数学家以及许多其他科学家感兴趣的,因为大多数系统本质上是非线性的。与更简单的线性系统形成对比,非线性系统可能会出现混乱,不可预测或违反直觉。通常,非线性系统的行为通过非线性方程组来描述,这是一组联立方程,其中未知量(或微分方程式的未知函数)出现为度数多项式的变量高于一个或一个不是一级多项式的函数的参数。由于非线性方程难以解决,非线性系统通常被线性方程(线性化)近似。这对于输入值有一定的准确性和一定的范围,但是一些有趣的现象,如孤子,混沌和奇异性被线性化隐藏。因此,非线性系统的行为的一些方面通常是反直觉的,不可预测的甚至是混乱的。一个实际的系统通常都会有某种不确定性,这种不确定性的因素,在系统的内外部都有可能发生。而这些不确定性因素往往是设计者不可预测的。面对这一事实,如何运用掌握的知识,设计出一个控制系统,使其能够达到预期的目标并有良好的控制效果,这就是反步控制将要研究和处理的问题。
因此,自上个世纪末以来,非线性系统的控制问题受到了国内外控制界的普遍关注与研究,尤其是在电力系统领域[5]。近几十年,随着微分代数系统的研究发展,非线性控制系统理论和研究应用都有了很好的发展。非线性控制系统理论在发展的进程中,有了许多新的内容,如Lyapunov稳定性方法、输入输出方法、精确线性化方法等[3]。除此之外, 针对一些运用其他控制理论不能很好达到目标的控制对象,近些年又提出了反步控制方法(Backstepping control)这一新的控制方法与理论[18]。
微分代数系统的概念在二十世纪七十年代初期被提出。基于其在科学工程领域的应用背景而在控制学方面受到了极大关注。近年来,在电网分析方面也提出了许多新的微分代数系统。
研究同步发电机非线性反步控制对于提高系统运行性能,从而加快我国电力系统方面的建设有一定的意义[5]。
1.2研究现状
同步发电机是一种比较特殊的交流发电机,由于其特殊的性能而被广泛用于各种发电场所。同步发电机在电力系统中的作用是当做电源使用,经过各种应用,同步发电机的优异性能得到了认可,因此,在电力系统中同步发电机具有支配地位。也正是由于这个原因,同步发电机在运动控制系统和电力设备中应用范围很广,如何对其有很可靠的控制效果也成为了学者们不断研究的项目。近年来,国内外学者为了提高同步发电机的控制性能,将一些研究出的新的非线性控制理论成果应用于同步发电机的控制,如状态反馈线性化控制、变结构控制、自适应控制以及本文将要讨论的反步控制[5]。
在控制理论中,反步控制是由Petar V.Kokotovic等人研究出的一种技术,用于为一些非线性系统设计稳定控制。这些系统是从可以使用其他方法稳定的不可约子系统辐射的子系统构建的。由于这种递归结构,设计人员可以在已知稳定的系统下启动设计过程,并“退出”逐步稳定每个外部子系统的新控制器。 当到达最终的外部控制时,这个过程就会停止。上述这个过程就被称为backstepping control[12],也就是反步控制。
反步控制理论自提出以来就表现出优异的控制效果,在解决非线性控制问题方面具有的优异性与独特性,近年来在工业控制领域处理某些非线性系统问题时得到大量的运用,也让国内外许多学者对其产生了很大的兴趣并加以研究。反步控制的基本原理是以Lyapunov稳定性判据为原则,在每一步的设计过程当中,选择相应的Lyapunov函数和虚拟控制函数,直到得到最终的控制函数。对于比较复杂的非线性系统,一般的设计方法并不能很好的解决,而反步控制则可以,具体的来说,反步控制的思想就是将上述系统分解成不超过该复杂系统阶次的子系统,而后用递推的方法构造出Lyapunov函数,保证子系统具有一定的收敛性并获得这个子系统的虚拟控制律;在构造设计下一个子系统的过程中,将上述的虚拟控制律作为这个子系统的跟踪目标。类似于上一个子系统的构造设计过程,推导出该子系统的虚拟控制律;然后不断按照这样的方法,直至得到整个闭环系统的实际控制律,并且运用Lyapunov稳定性判据方法,确保整个闭环系统的收敛性[10]。该方法以保证系统一致渐近稳定为原则,对于整个系统的全局稳定性具有一定的保障。
1.3 主要工作
基于微分代数系统,针对同步发电机控制系统,研究非线性反步控制问题,在无干扰带有未知参数的情况下,设计出一个非线性控制器,设计出的控制器要能够使得同步发电机闭环系统渐近稳定。然后运用MATLAB进对同步发电机控制系统行系统仿真,来验证本文方法的正确性和有效性。
2 预备知识
2.1 微分代数系统
由微分方程和代数方程组合而成的系统成为微分代数系统(DAE系统),也叫作微分代数方程。该系统能更精确的描述真实物理运动现象。通常用下边这样的方程来描述一个微分代数系统:
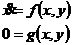 (2.1)
(2.1)
式中,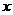 是微分变量,
是微分变量,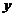 是代数变量,
是代数变量,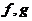 均为光滑映射。
均为光滑映射。
2.2 非线性系统
可以用下边这个微分方程来代表一个非线性系统[1]:
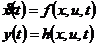 (2.2)
(2.2)
在上边这个式子中,状态向量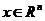 ;输出向量
;输出向量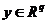 ;输入向量
;输入向量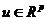 ;
;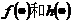 为相应维数的向量函数。式(2.2)中,第一个式子叫做系统的状态方程,第二个式子叫做系统的输出方程。
为相应维数的向量函数。式(2.2)中,第一个式子叫做系统的状态方程,第二个式子叫做系统的输出方程。
需要说明的是,对式(2.2)所描述的非线性系统,假定系统的状态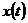 可由初始值
可由初始值 和输入函数
和输入函数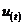 唯一的确定。
唯一的确定。
2.3 Lyapunov稳定性定义
考察如下的时不变非线性系统[1]
剩余内容已隐藏,请支付后下载全文,论文总字数:24486字
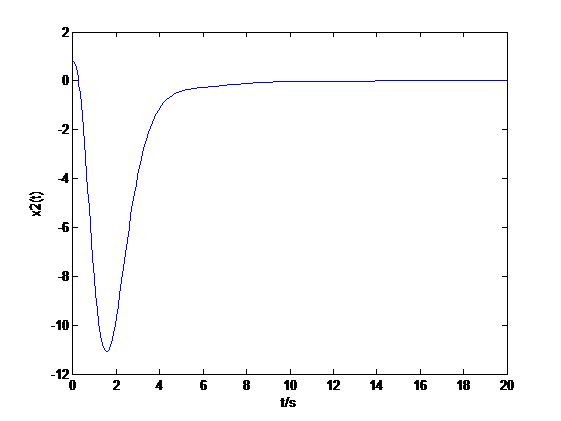
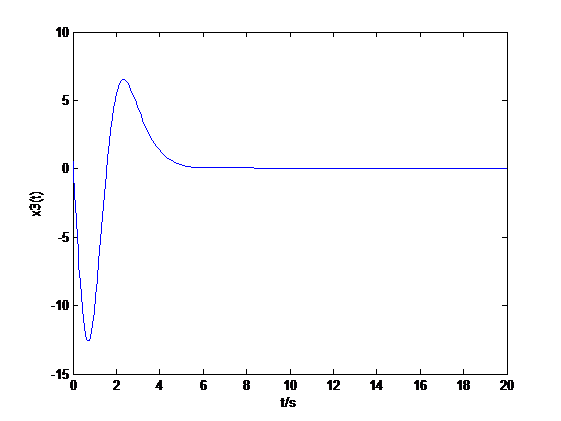
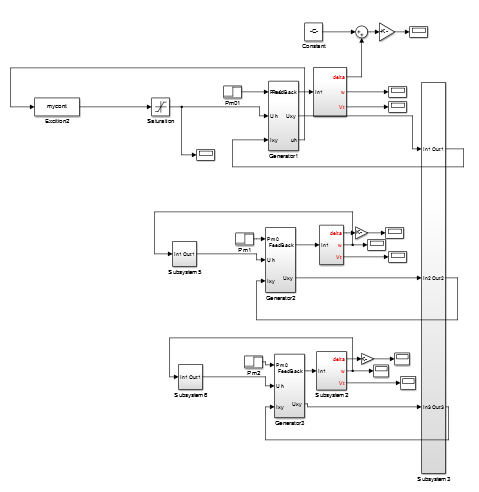
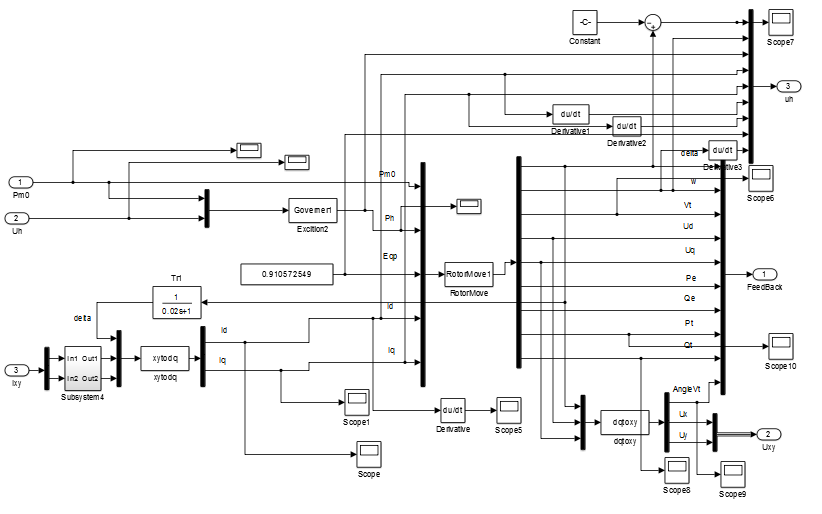
相关图片展示:

该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


